Section 3.11 : Related Rates
6. A plane is 750 meters in the air flying parallel to the ground at a speed of 100 m/s and is initially 2.5 kilometers away from a radar station. At what rate is the distance between the plane and the radar station changing (a) initially and (b) 30 seconds after it passes over the radar station?

Show All Solutions Hide All Solutions
a At what rate is the distance between the plane and the radar station changing initially? Show All Steps Hide All StepsStart Solution
For this part we know that \(x' = - 100\) when \(x = 2500\). In this case note that \(x'\) must be negative because \(x\) will be decreasing in this part. Also note that we converted \(x\) to meters since all the other quantities are in meters.
Here is a sketch for this part.
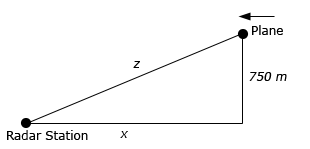
We want to determine \(z'\) in this part so using the Pythagorean Theorem we get the following equation to relate \(x\) and \(z\).
\[{z^2} = {x^2} + {750^2} = {x^2} + 562500\] Show Step 3Finally, let’s differentiate this with respect to \(t\) and we can even solve it for \(z'\) so the actual solution will be quick and simple to find.
\[2z\,z' = 2x\,x'\hspace{0.5in} \Rightarrow \hspace{0.5in}z' = \frac{{x\,x'}}{z}\] Show Step 3To finish off this problem all we need to do is determine \(z\) (reusing the Pythagorean Theorem) and then plug into the equation from Step 3 above.
\[z = \sqrt {{{2500}^2} + {{750}^2}} = \sqrt {6812500} = 250\sqrt {109} = 2610.0766\]The rate of change of the distance between the two for this part is,
\[z' = \frac{{\left( {2500} \right)\left( { - 100} \right)}}{{2610.0766}} = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 95.7826}}\]b At what rate is the distance between the plane and the radar station changing 30 seconds after it passes over the radar station? Show All Steps Hide All Steps
Start Solution
For this part we know that \(x' = 100\) and it will be positive in this case because \(x\) will now be increasing as we can see in the sketch below.
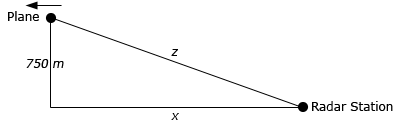
As with the previous part we want to determine \(z'\) and equation we’ll need is identical to the previous part so we’ll just rewrite both it and its derivative here.
\[\begin{array}{c}{z^2} = {x^2} + {750^2} = {x^2} + 562500\\ 2z\,z' = 2x\,x'\hspace{0.5in} \Rightarrow \hspace{0.5in}z' = \frac{{x\,x'}}{z}\end{array}\] Show Step 3To finish off this problem all we need to do is determine both \(x\) and \(z\). For \(x\) we know the speed of the plane and the fact that it has flown for 30 seconds after passing over the radar station. So \(x\) is,
\[x = \left( {100} \right)\left( {30} \right) = 3000\]For \(z\) we just need to reuse the Pythagorean Theorem.
\[z = \sqrt {{{3000}^2} + {{750}^2}} = \sqrt {9562500} = 750\sqrt {17} = 3092.3292\]The rate of change of the distance between the two for this part is then,
\[z' = \frac{{\left( {3000} \right)\left( {100} \right)}}{{3092.3292}} = \require{bbox} \bbox[2pt,border:1px solid black]{{97.0143}}\]