Section 3.11 : Related Rates
11. The angle of elevation is the angle formed by a horizontal line and a line joining the observer’s eye to an object above the horizontal line. A person is 500 feet way from the launch point of a hot air balloon. The hot air balloon is starting to come back down at a rate of 15 ft/sec. At what rate is the angle of elevation, \(\theta \), changing when the hot air balloon is 200 feet above the ground.
Show All Steps Hide All Steps
Start SolutionPutting variables and known quantities on the sketch from the problem statement gives,
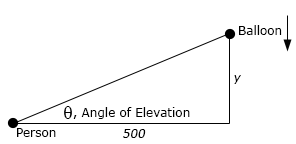
We want to determine \(\theta '\) when \(y = 200\) and we know that \(y' = - 15\).
Show Step 2There are a variety of equations that we could use here but probably the best one that involves all of the known and needed quantities is,
\[\tan \left( \theta \right) = \frac{y}{{500}}\] Show Step 3Differentiating with respect to \(t\) gives,
\[{\sec ^2}\left( \theta \right)\,\,\theta ' = \frac{{y'}}{{500}}\hspace{0.5in} \Rightarrow \hspace{0.5in}\theta ' = \frac{{y'}}{{500}}{\cos ^2}\left( \theta \right)\] Show Step 4To finish off this problem all we need to do is determine the value of \(\theta \) for the time in question. We can either use the original equation to do this or we could acknowledge that all we really need is \(\cos \left( \theta \right)\) and we could do a little right triangle trig to determine that.
For this problem we’ll just use the original equation to find the value of \(\theta \).
\[\tan \left( \theta \right) = {\textstyle{{200} \over {500}}}\hspace{0.5in} \Rightarrow \hspace{0.5in}\theta = {\tan ^{ - 1}}\left( {{\textstyle{2 \over 5}}} \right) = 0.38051\,{\mbox{radians}}\]The rate of change of the angle of elevation is then,
\[\theta ' = \frac{{ - 15}}{{500}}{\cos ^2}\left( {0.38051} \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 0.02586}}\]