Section 9.1 : Parametric Equations and Curves
4. Eliminate the parameter for the following set of parametric equations, sketch the graph of the parametric curve and give any limits that might exist on \(x\) and \(y\).
\[x = 3\sin \left( t \right)\hspace{0.5in}y = - 4\cos \left( t \right)\hspace{0.25in}\hspace{0.5in}\,\,\,\,\,0 \le t \le 2\pi \]Show All Steps Hide All Steps
Start SolutionFirst, we’ll eliminate the parameter from this set of parametric equations. For this particular set of parametric equations we will make use of the well-known trig identity,
\[{\cos ^2}\left( \theta \right) + {\sin ^2}\left( \theta \right) = 1\]We can solve each of the parametric equations for sine and cosine as follows,
\[\sin \left( t \right) = \frac{x}{3}\hspace{0.25in}\hspace{0.25in}\cos \left( t \right) = - \frac{y}{4}\]Plugging these into the trig identity gives,
\[{\left( { - \frac{y}{4}} \right)^2} + {\left( {\frac{x}{3}} \right)^2} = 1\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{16}} = 1\]Therefore, the parametric curve will be some or all of the ellipse above.
We have to be careful when eliminating the parameter from a set of parametric equations. The graph of the resulting equation in only \(x\) and \(y\) may or may not be the graph of the parametric curve. Often, although not always, the parametric curve will only be a portion of the curve from the equation in terms of only \(x\) and \(y\). Another situation that can happen is that the parametric curve will retrace some or all of the curve from the equation in terms of only \(x\) and \(y\) more than once.
The next few steps will help us to determine just how much of the ellipse we have and if it retraces the ellipse, or a portion of the ellipse, more than once.
Before we proceed with the rest of the problem let’s fist note that there is really no set order for doing the steps. They can often be done in different orders and in some cases may actually be easier to do in different orders. The order we’ll be following here is used simply because it is the order that I’m used to working them in. If you find a different order would be best for you then that is the order you should use.
Show Step 2At this point we can get a good idea on what the limits on \(x\) and \(y\) are going to be so let’s do that. Note that often we won’t get the actual limits on \(x\) and \(y\) in this step. All we are really finding here is the largest possible range of limits for \(x\) and \(y\). Having these can sometimes be useful for later steps and so we’ll get them here.
We can use our knowledge of sine and cosine to get the following inequalities. Note as discussed above however that these may not be the limits on \(x\) and \(y\) we are after.
\[\begin{array}{ccc} - 1 \le \sin \left( t \right) \le 1 & \hspace{1.0in} & - 1 \le \cos \left( t \right) \le 1\\ - 3 \le 3\sin \left( t \right) \le 3 & \hspace{1.0in} & 4 \ge - 4\cos \left( t \right) \ge - 4\\ - 3 \le x \le 3 & \hspace{1.0in} & - 4 \le y \le 4\end{array}\]Note that to find these limits in general we just start with the appropriate trig function and then build up the equation for \(x\) and \(y\) by first multiplying the trig function by any coefficient, if present, and then adding/subtracting any numbers that might be present (not needed in this case). This, in turn, gives us the largest possible set of limits for \(x\) and \(y\). Just remember to be careful when multiplying an inequality by a negative number. Don’t forget to flip the direction of the inequalities when doing this.
Now, at this point we need to be a little careful. What we’ve actually found here are the largest possible inequalities for the limits on \(x\) and \(y\). This set of inequalities for the limits on \(x\) and \(y\) assume that the parametric curve will be completely traced out at least once for the range of \(t\)’s we were given in the problem statement. It is always possible that the curve will not trace out a full trace in the given range of \(t\)’s. In a later step we’ll determine if the parametric curve does trace out a full trace and hence determine the actual limits on \(x\) and \(y\).
Before we move onto the next step there are a couple of issues we should quickly discuss.
First, remember that when we talk about the parametric curve tracing out once we are not necessarily talking about the ellipse itself being fully traced out. The parametric curve will be at most the full ellipse and we haven’t determined just yet how much of the ellipse the parametric curve will trace out. So, one trace of the parametric curve refers to the largest portion of the ellipse that the parametric curve can possibly trace out given no restrictions on \(t\).
Second, if we can’t completely determine the actual limits on \(x\) and \(y\) at this point why did we do them here? In part we did them here because we can and the answer to this step often does end up being the limits on \(x\) and \(y\). Also, there are times where knowing the largest possible limits on \(x\) and/or \(y\) will be convenient for some of the later steps.
Finally, we can sometimes get these limits from the sketch of the parametric curve. However, there are some parametric equations that we can’t easily get the sketch without doing this step. We’ll eventually do some problems like that.
Show Step 3Before we sketch the graph of the parametric curve recall that all parametric curves have a direction of motion, i.e. the direction indicating increasing values of the parameter, \(t\) in this case.
There are several ways to get the direction of motion for the curve. One is to plug in values of \(t\) into the parametric equations to get some points that we can use to identify the direction of motion.
Here is a table of values for this set of parametric equations. In this case we were also given a range of \(t\)’s and we need to restrict the \(t\)’s in our table to that range.
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| 0 | 0 | -4 |
| \(\frac{\pi }{2}\) | 3 | 0 |
| \(\pi \) | 0 | 4 |
| \(\frac{{3\pi }}{2}\) | -3 | 0 |
| \(2\pi \) | 0 | -4 |
Now, this table seems to suggest that the parametric equation will follow the ellipse in a counter clockwise rotation. It also seems to suggest that the ellipse will be traced out exactly once.
However, tables of values for parametric equations involving sine and/or cosine equations can be deceptive.
Because sine and cosine oscillate it is possible to choose “bad” values of \(t\) that suggest a single trace when in fact the curve is tracing out faster than we realize and it is in fact tracing out more than once. We’ll need to do some extra analysis to verify if the ellipse traces out once or more than once.
Also, just because the table suggests a particular direction doesn’t actually mean it is going in that direction. It could be moving in the opposite direction at a speed that just happens to match the points you got in the table. Go back to the notes and check out Example 5. Plug in the points we used in our table above and you’ll get a set of points that suggest the curve is tracing out clockwise when in fact it is tracing out counter clockwise!
Note that because this is such a “bad” way of getting the direction of motion we put it in its own step so we could discuss it in detail. The actual method we’ll be using is in the next step and we’ll not be doing table work again unless it is absolutely required for some other part of the problem.
Show Step 4As suggested in the previous step the table of values is not a good way to get direction of motion for parametric curves involving trig function so let’s go through a much better way of determining the direction of motion. This method takes a little time to think things through but it will always get the correct direction if you take the time.
First, let’s think about what happens if we start at \(t = 0\) and increase \(t\) to \(t = \pi \).
As we cover this range of \(t\)’s we know that cosine starts at 1, decreasing through zero and finally stops at -1. So, that means that \(y\) will start at \(y = - 4\) (i.e. where cosine is 1), go through the \(x\)-axis (i.e. where cosine is zero) and finally stop at \(y = 4\) (i.e. where cosine is -1). Now, this doesn’t give us a direction of motion as all it really tells us that \(y\) increases and it could do this following the right side of the ellipse (i.e. counter clockwise) or it could do this following the left side of the ellipse (i.e. clockwise).
So, let’s see what the behavior of sine in this range tells us. Starting at \(t = 0\) we know that sine will be zero and so \(x\) will also be zero. As \(t\) increases to \(t = \frac{\pi }{2}\) we know that sine increases from zero to one and so \(x\) will increase from zero to three. Finally, as we further increase \(t\) to \(t = \pi \) sine will decrease from one back to zero and so \(x\) will also decrease from three to zero.
So, taking the \(x\) and \(y\) analysis above together we can see that at \(t = 0\) the curve will start at the point \(\left( {0, - 4} \right)\). As we increase \(t\) to \(t = \frac{\pi }{2}\) the curve will have to follow the ellipse with increasing \(x\) and \(y\) until it hits the point \(\left( {3,0} \right)\). The only way we can reach this second point and have the correct increasing behavior for both \(x\) and \(y\) is to move in a counter clockwise direction along the right half of the ellipse.
If we further increase \(t\) from \(t = \frac{\pi }{2}\) to \(t = \pi \) we can see that \(y\) must continue to increase but \(x\) now decreases until we get to the point \(\left( {0,4} \right)\) and again the only way we can reach this third point and have the required increasing/decreasing information for \(y\)/\(x\) respectively is to be moving in a counter clockwise direction along the right half.
We can do a similar analysis increasing \(t\) from \(t = \pi \) to \(t = 2\pi \) to see that we must still move in a counter clockwise direction that takes us through the point \(\left( { - 3,0} \right)\) and then finally ending at the point \(\left( {0, - 4} \right)\).
So, from this analysis we can see that the curve must be tracing out in a counter clockwise direction.
This analysis seems complicated and maybe not so easy to do the first few times you see it. However, once you do it a couple of times you’ll see that it’s not quite as bad as it initially seems to be. Also, it really is the only way to guarantee that you’ve got the correct direction of motion for the curve when dealing with parametric equations involving sine and/or cosine.
If you had trouble visualizing how sine and cosine changed as we increased \(t\) you might want to do a quick sketch of the graphs of sine and cosine and you’ll see right away that we were correct in our analysis of their behavior as we increased \(t\).
Show Step 5Okay, in the last step notice that we also showed that the curve will trace the ellipse out exactly once in the given range of \(t\)’s. However, let’s assume that we hadn’t done the direction analysis yet and see if we can determine this without the direction analysis.
This is actually pretty simple to do, or at least simpler than the direction analysis. All it requires is that you know where sine and cosine are zero, 1 and -1. If you recall your unit circle it’s always easy to know where sine and cosine have these values. We’ll also be able to verify the ranges of \(x\) and \(y\) found in Step 2 were in fact the actual ranges for \(x\) and \(y\).
Let’s start with the “initial” point on the curve, i.e. the point at the left end of our range of \(t\)’s, \(t = 0\) in this case. Where you start this analysis is really dependent upon the set of parametric equations, the parametric curve and/or if there is a range of \(t\)’s given. Good starting points are the “initial” point, one of the end points of the curve itself (if the curve does have endpoints) or \(t = 0\). Sometimes one option will be better than the others and other times it won’t matter.
In this case two of the options are the same point so it seems like a good point to use.
So, at \(t = 0\) we are at the point \(\left( {0, - 4} \right)\). We know that the parametric curve is some or all of the ellipse we found in the first step. So, at this point let’s assume it is the full ellipse and ask ourselves the following question. When do we get back to this point? Or, in other words, what is the next value of \(t\) after \(t = 0\) (since that is the point we choose to start off with) are we back at the point \(\left( {0, - 4} \right)\)?
Before doing this let’s quickly note that if the parametric curve doesn’t get back to this point we’ll determine that in the following analysis and that will be useful in helping us to determine how much of the ellipse will get traced out by the parametric curve.
Okay let’s back to the analysis. In order to be at the point \(\left( {0, - 4} \right)\) we know we must have \(\sin \left( t \right) = 0\) (only way to get \(x = 0\)!) and we must have \(\cos \left( t \right) = 1\) (only way to get \(y = - 4\)!). For \(t > 0\) we know that \(\sin \left( t \right) = 0\) at \(t = \pi ,2\pi ,3\pi , \ldots \) and likewise we know that \(\cos \left( t \right) = 1\) at \(t = 2\pi ,4\pi ,6\pi , \ldots \). The first value of \(t\) that is in both lists is \(t = 2\pi \) and so this is the next value of \(t\) that will put us at that point.
This tells us several things. First, we found that the parametric equation will get back to the initial point and so it is possible for the parametric equation to trace out the full ellipse.
Secondly, we got back to the point \(\left( {0, - 4} \right)\) at the very last \(t\) from the range of \(t\)’s we were given in the problem statement and so the parametric curve will trace out the ellipse exactly once for the given range of \(t\)’s.
Finally, from this analysis we found the parametric curve traced out the full ellipse in the range of \(t\)’s given in the problem statement and so we know now that the limits of \(x\) and \(y\) we found in Step 2 are in fact the actual limits on \(x\) and \(y\) for this curve.
As a final comment from this step let’s note that this analysis in this step was a little easier than normal because the argument of the trig functions was just a \(t\) as opposed to say 2\(t\) or \(\frac{1}{3}t\) which does make the analysis a tiny bit more complicated. We’ll see how to deal with these kinds of arguments in the next couple of problems.
Show Step 6Finally, here is a sketch of the parametric curve for this set of parametric equations.
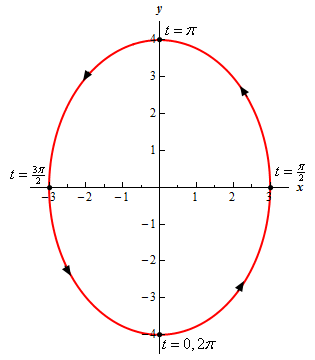
For this sketch we included the points from our table because we had them but we won’t always include them as we are often only interested in the sketch itself and the direction of motion.
Also, because the problem asked for it here are the formal limits on \(x\) and \(y\) for this parametric curve.
\[ - 3 \le x \le 3\hspace{0.25in}\hspace{0.25in} - 4 \le y \le 4\]As a final set of thoughts for this problem you really should go back and make sure you understand the processes we went through in Step 4 and Step 5. Those are often the best way of getting at the information we found in those steps. The processes can seem a little mysterious at first but once you’ve done a couple you’ll find it isn’t as bad as they might have first appeared.
Also, for the rest of the problems in this section we’ll build a table of \(t\) values only if it is absolutely necessary for the problem. In other words, the process we used in Step 4 and 5 will be the processes we’ll be using to get direction of motion for the parametric curve and to determine if the curve is traced out more than once or not.
You should also take a look at problems 5 and 6 in this section and contrast the number of traces of the curve with this problem. The only difference in the set of parametric equations in problems 4, 5 and 6 is the argument of the trig functions. After going through these three problems can you reach any conclusions on how the argument of the trig functions will affect the parametric curves for this type of parametric equations?