Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 13.6 : Chain Rule
5. Given the following information use the Chain Rule to determine \({z_t}\) and \({z_p}\) .
\[z = 4y\sin \left( {2x} \right)\,\hspace{0.5in}x = 3u - p,\,\,\,\,y = {p^2}u,\,\,\,\,\,\,u = {t^2} + 1\]Show All Steps Hide All Steps
Start SolutionOkay, we don’t have a formula from the notes for this one so we’ll need to derive on up first. To do this we’ll need the following tree diagram.
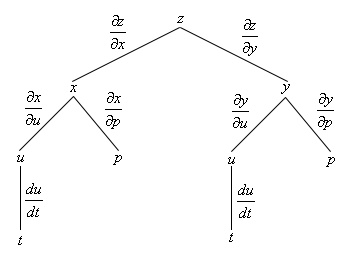
Here are the formulas for the two derivatives we’re being asked to find.
\[{z_t} = \frac{{\partial z}}{{\partial t}} = \frac{{\partial z}}{{\partial x}}\frac{{\partial x}}{{\partial u}}\frac{{du}}{{dt}} + \frac{{\partial z}}{{\partial y}}\frac{{\partial y}}{{\partial u}}\frac{{du}}{{dt}}\hspace{0.5in}{z_p} = \frac{{\partial z}}{{\partial p}} = \frac{{\partial z}}{{\partial x}}\frac{{\partial x}}{{\partial p}} + \frac{{\partial z}}{{\partial y}}\frac{{\partial y}}{{\partial p}}\] Show Step 3Here is the work for this problem.
\[\begin{align*}{z_t} & = \frac{{\partial z}}{{\partial x}}\frac{{\partial x}}{{\partial u}}\frac{{du}}{{dt}} + \frac{{\partial z}}{{\partial y}}\frac{{\partial y}}{{\partial u}}\frac{{du}}{{dt}}\\ & = \left[ {8y\cos \left( {2x} \right)} \right]\left[ 3 \right]\left[ {2t} \right] + \left[ {4\sin \left( {2x} \right)} \right]\left[ {{p^2}} \right]\left[ {2t} \right]\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{48ty\cos \left( {2x} \right) + 8t{p^2}\sin \left( {2x} \right)}}\end{align*}\] \[\begin{align*}{z_p} & = \frac{{\partial z}}{{\partial x}}\frac{{\partial x}}{{\partial p}} + \frac{{\partial z}}{{\partial y}}\frac{{\partial y}}{{\partial p}}\\ & = \left[ {8y\cos \left( {2x} \right)} \right]\left[ { - 1} \right] + \left[ {4\sin \left( {2x} \right)} \right]\left[ {2pu} \right]\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 8y\cos \left( {2x} \right) + 8pu\sin \left( {2x} \right)}}\end{align*}\]In the second step of each of the derivatives we added brackets just to make it clear which term came from which derivative in the “formula”.
Also, we didn’t do any “back substitution” in these derivatives due to the mess that we’d get from each of the derivatives after we got done with all the back substitution.