Section 13.6 : Chain Rule
6. Given the following information use the Chain Rule to determine \(\displaystyle \frac{{\partial w}}{{\partial t}}\) and \(\displaystyle \frac{{\partial w}}{{\partial s}}\) .
\[w = \sqrt {{x^2} + {y^2}} + \frac{{6z}}{y}\,\hspace{0.5in}x = \sin \left( p \right),\,\,\,\,y = p + 3t - 4s,\,\,\,\,z = \frac{{{t^3}}}{{{s^2}}},\,\,\,\,p = 1 - 2t\]Show All Steps Hide All Steps
Start SolutionOkay, we don’t have a formula from the notes for this one so we’ll need to derive on up first. To do this we’ll need the following tree diagram.
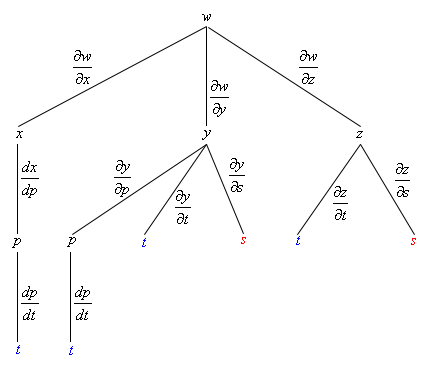
Some of these tree diagrams can get quite messy. We’ve colored the variables we’re interested in to try and make the branches we need to follow for each derivative a little clearer.
Show Step 2Here are the formulas for the two derivatives we’re being asked to find.
\[\frac{{\partial w}}{{\partial t}} = \frac{{\partial w}}{{\partial x}}\frac{{dx}}{{dp}}\frac{{dp}}{{dt}} + \frac{{\partial w}}{{\partial y}}\frac{{\partial y}}{{\partial p}}\frac{{dp}}{{dt}} + \frac{{\partial w}}{{\partial y}}\frac{{\partial y}}{{\partial t}} + \frac{{\partial w}}{{\partial z}}\frac{{\partial z}}{{\partial t}}\hspace{0.5in}\frac{{\partial w}}{{\partial s}} = \frac{{\partial w}}{{\partial y}}\frac{{\partial y}}{{\partial s}} + \frac{{\partial w}}{{\partial z}}\frac{{\partial z}}{{\partial s}}\] Show Step 3Here is the work for this problem.
\[\begin{align*}\frac{{\partial w}}{{\partial t}} & = \frac{{\partial w}}{{\partial x}}\frac{{dx}}{{dp}}\frac{{dp}}{{dt}} + \frac{{\partial w}}{{\partial y}}\frac{{\partial y}}{{\partial p}}\frac{{dp}}{{dt}} + \frac{{\partial w}}{{\partial y}}\frac{{\partial y}}{{\partial t}} + \frac{{\partial w}}{{\partial z}}\frac{{\partial z}}{{\partial t}}\\ & = \left[ {\frac{x}{{\sqrt {{x^2} + {y^2}} }}} \right]\left[ {\cos \left( p \right)} \right]\left[ { - 2} \right] + \left[ {\frac{y}{{\sqrt {{x^2} + {y^2}} }} - \frac{{6z}}{{{y^2}}}} \right]\left[ 1 \right]\left[ { - 2} \right] + \\ & \hspace{0.5in}\hspace{0.5in}\hspace{0.25in}\,\,\,\,\,\,\, + \left[ {\frac{y}{{\sqrt {{x^2} + {y^2}} }} - \frac{{6z}}{{{y^2}}}} \right]\left[ 3 \right] + \left[ {\frac{6}{y}} \right]\left[ {\frac{{3{t^2}}}{{{s^2}}}} \right]\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{ - 2x\cos \left( p \right)}}{{\sqrt {{x^2} + {y^2}} }} + \frac{y}{{\sqrt {{x^2} + {y^2}} }} - \frac{{6z}}{{{y^2}}} + \frac{{18{t^2}}}{{y{s^2}}}}}\end{align*}\] \[\begin{align*}\frac{{\partial w}}{{\partial s}} & = \frac{{\partial w}}{{\partial y}}\frac{{\partial y}}{{\partial s}} + \frac{{\partial w}}{{\partial z}}\frac{{\partial z}}{{\partial s}}\\ & = \left[ {\frac{y}{{\sqrt {{x^2} + {y^2}} }} - \frac{{6z}}{{{y^2}}}} \right]\left[ { - 4} \right] + \left[ {\frac{6}{y}} \right]\left[ { - \frac{{2{t^3}}}{{{s^3}}}} \right]\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{ - 4y}}{{\sqrt {{x^2} + {y^2}} }} + \frac{{24z}}{{{y^2}}} - \frac{{12{t^3}}}{{y{s^3}}}}}\end{align*}\]In the second step of each of the derivatives we added brackets just to make it clear which term came from which derivative in the “formula” and in general probably aren’t needed. We also did a little simplification as needed to get to the third step.
Also, we didn’t do any “back substitution” in these derivatives due to the mess that we’d get from each of the derivatives after we got done with all the back substitution.