Section 15.8 : Change of Variables
10. Derive the transformation used in problem 8.
Show All Steps Hide All Steps
Start SolutionOkay, for reference purposes we want to derive the following transformation,
\[x = \frac{1}{3}\left( {v - u} \right)\hspace{0.25in}\hspace{0.25in}y = \frac{1}{3}\left( {4v - u} \right)\]We used this transformation on the following region.
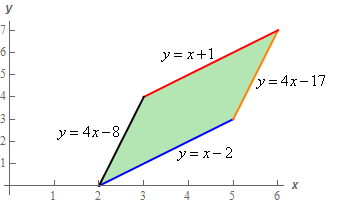
The result of the applying the transformation to the region above got us the following “new” region.
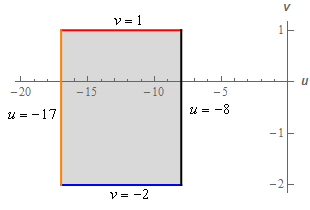
We need to derive the transformation. This seems to be a nearly impossible task at first glance. However, it isn’t as difficult as it might appear to be. Or maybe we should say it won’t be as difficult as it seems to be once you see how to do it.
Before we start with the derivation process we should point out that there are actually quite a few possible transformations that we could use on the original region and get a rectangle for the new region. They won’t however all yield the same rectangle. We are going to get a specific transformation but you should be able how to modify what we’re doing here to get a different transformation.
Show Step 2The first thing that we’re going to do is rewrite all the boundary equations for the original region as follows.
\[\begin{align*}y & = x + 1\hspace{0.25in}\hspace{0.25in} \to \hspace{0.25in}\hspace{0.25in}y - x = 1\\ y & = 4x - 17\hspace{0.25in}\hspace{0.25in} \to \hspace{0.25in}\hspace{0.25in}y - 4x = - 17\\ y & = x - 2\hspace{0.25in}\hspace{0.25in} \to \hspace{0.25in}\hspace{0.25in}y - x = - 2\\ y & = 4x - 8\hspace{0.25in}\hspace{0.25in} \to \hspace{0.25in}\hspace{0.25in}y - 4x = - 8\end{align*}\]Now, let’s notice that because our original region had two sets of parallel sides our new equations can also be organized into two pairs of equations as follows,
\[\begin{align*}y - x & = 1\hspace{0.25in}\hspace{0.25in}{\mbox{AND}}\hspace{0.25in}\hspace{0.25in}y - x = - 2\\ y - 4x & = - 17\hspace{0.25in}\hspace{0.25in}{\mbox{AND}}\hspace{0.25in}\hspace{0.25in}y - 4x = - 8\end{align*}\]The left side of each pair of equations is identical (i.e. they came from parallel sides of our original region). This is going to make life easier for us in order to derive a derivation that will give a “nice” region. Of course, in this case, we already know what the new region is going to be but in general we wouldn’t.
Show Step 3Now, we want to define new variables \(u\) and \(v\) in terms of the old variables \(x\) and \(y\) in such a way that we will get the rectangle we are looking for.
Let’s define \(u\) and \(v\) as follows (we’ll explain why in a bit),
\[u = y - 4x\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}v = y - x\]With this definition note that we can already see what our “new” region will be. Putting these definitions into the equations we wrote down in Step 2 gives us,
\[\begin{align*}v & = 1\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}{\mbox{AND}}\hspace{0.25in}\hspace{0.25in}v = - 2\\ u & = - 17\hspace{0.25in}\hspace{0.25in}{\mbox{AND}}\hspace{0.25in}\hspace{0.25in}u = - 8\end{align*}\]This is exactly the new region that we got in Problem 8. This tells us that we’ll get the transformation in Problem 8 from this definition (we’ll do that work in the next step).
It should also make it a little clearer why we chose the definitions of \(u\) and \(v\) as we did above. We know that we wanted an easier region to integration over and let’s be honest a rectangle is really easy to integrate over so trying to get a rectangle for the new region seemed like a good idea.
This is where the two pairs of equations comes into play. Because we were able to pair up the equations so the left side was identical in each pair all we had to do was define one of the left sides as \(u\) and the other as \(v\) and we would know at that point that we’d get a rectangle as our new region.
Note however, that it should also now be clear that there would be another “simple” definition for \(u\) and \(v\) that we could have used (i.e. \(u = y - x\), \(v = y - 4x\)). It would have resulted in a similar, yet different, rectangle and a different transformation. There was no real reason for choosing our definition of \(u\) and \(v\) as we did over the other possibility other than we knew the region we wanted to get. Back in Problem 8 we basically just chose one at random.
Now, there are probably quite a few questions in your mind at this point and we’ll address as many of them as we can in the last step. Let’s finish the actual problem out first before we do that however just so we don’t forget what we’re doing here.
Show Step 4Okay, let’s finish the actual problem before we answer some questions in the final step. We need to use our definition of \(u\) and \(v\) from the last step to get the transformation we used in Problem 8.
First, let’s just start off with our definition of \(u\) and \(v\) again.
\[\begin{align*}u & = y - 4x\\ v & = y - x\end{align*}\]Now, what we have here is a system of two equations. All we need to do to finish this problem out is solve them for \(x\) and \(y\).
To do this let’s first solve the \(v\) definition for \(y\).
\[v = y - x\,\,\,\hspace{0.25in}\to \hspace{0.25in}\,\,\,\,\,y = v + x\]Plug this into the \(u\) definition and solve for \(x\).
\[u = y - 4x\hspace{0.25in}\to \hspace{0.25in}\,\,u = v + x - 4x = v - 3x\,\,\,\,\,\,\,\,\,\, \to \hspace{0.25in}x = \frac{1}{3}\left( {v - u} \right)\]That should look familiar of course. Now, all we need to do is find the \(y\) transformation. To do this we’ll just plug our \(x\) transformation into \(y = v + x\) and do a little simplification.
\[y = v + x = v + \frac{1}{3}\left( {v - u} \right) = \frac{4}{3}v - \frac{1}{3}u = \frac{1}{3}\left( {4v - u} \right)\]So, there we go. The transformation has been derived and now that you see how to do it we can see that it wasn’t really all that bad despite first appearances.
Show Step 5Okay, now let’s see if we can address at least some of the questions you might have about deriving transformations.
Can we always transform any region into a rectangle?
The short answer is definitely NO. In order to quickly get a transformation that yielded a rectangle here we relied on the fact that we had an original region that had four linear sides and we were able to form them into two pairs of parallel sides. Once that was done it was easy to get a transformation that would yield a rectangle.
Many regions can’t be transformed (or at least not easily transformed) into a rectangle.
So, what if we’d had a region with four linear sides but we couldn’t form them into two sets of parallel sides?
In this case the problem would still work pretty much the same way but we’d have lots more options for definition of \(u\) and \(v\) and the result wouldn’t be a rectangle.
In a case like this, because all the sides are linear, we can still write each of them in as follows,
\[\begin{align*}& {\mbox{Side 1 : }}{a_1}y + {b_1}x = {c_1}\\ & {\mbox{Side 2 : }}{a_2}y + {b_2}x = {c_2}\\ & {\mbox{Side 3 : }}{a_3}y + {b_3}x = {c_3}\\ & {\mbox{Side 4 : }}{a_4}y + {b_4}x = {c_4}\end{align*}\]At this point we could define \(u\) to be any of the left sides and \(v\) to be any other remaining left sides. This would guarantee one side will be vertical and one side will be horizontal in the new region. The remaining two sides of the original region would then be transformed into new lines and hopefully the resulting region would be easy to work with.
As you can see there would be lots of possible definitions of \(u\) and \(v\) here which in turn would lead to lots of different transformations.
What if you had more or less than four linear sides?
The process described in this problem should still work to derive a transformation. Whether or not the resulting region is easy to integrate over may be a completely different questions however and there won’t necessarily be any way to know until you’ve derived the transformation and done the work to get the new region.
What if you had at least one side that was not linear?
With these types of regions then the process described in this problem may still work but it also might not. It will depend on just how “messy” the equation of the non-linear boundary is and if we can even solve the definitions of \(u\) and \(v\) for \(x\) and \(y\) as we did in Step 4 of this problem.
Unfortunately, there really isn’t any good answer to this question. There are many ways of getting transformations. We’ve simply described one of the easier methods of deriving a transformation for the type of regions that you’re most likely to run into in this class. The method will work on occasion for regions that have one or more non-linear boundary but there is no reason to expect it to work with every possible region.
Are all transformations derived in this fashion?
As alluded to in the answer to the previous question, absolutely not. There are many types of regions where this process simply won’t work, or at least won’t work easily.
A good example is the ellipse we looked at in Problem 4. If you’ve done that problem then you’ll probably already know that you can pretty much get a transformation that will transform the ellipse into a circle by inspection. The process described in this problem simply won’t work on that region.
The point of this problem was not to teach you now to derive transformations in general. It was simply to show you how many of the transformations in these problems were derived and to show you one method that, when it can be used, is fairly simple to do.
Are there any variations to this derivation method?
Absolutely. See the next problem for at least one.