Section 15.8 : Change of Variables
11. Derive a transformation that will convert the triangle with vertices \(\left( {1,0} \right)\), \(\left( {6,0} \right)\) and \(\left( {3,8} \right)\) into a right triangle with the right angle occurring at the origin of the \(uv\) system.
Show All Steps Hide All Steps
Start SolutionWe’re going to be using slight modification of the process used in the previous problem here. If you haven’t read through that problem you should before proceeding with this problem as we’re not going to be going over the explanation in quite as much detail here.
So, let’s just start off with a sketch of the triangle.
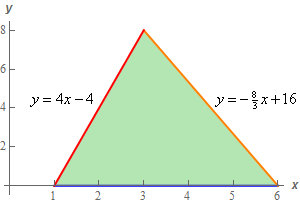
We’ll leave it to you to verify the algebra details of deriving the equations of the two sloped sides. The bottom side is of course just defined by \(y = 0\).
Show Step 2This region is clearly a little different from the region in the previous problem but the next step is still the same. We start with writing the equations of each of the sides as follows.
\[\begin{align*}y - 4x & = - 4\\ y + \frac{8}{3}x & = 16\\ y & = 0\end{align*}\]Again, what we simply put all the variables on one side and the constant on the other. We also aren’t going to worry about the fact that the third equation doesn’t have an \(x\). Not only will that not be a problem it actually is going to make this problem a little easier.
Show Step 3Now, if we followed the process from the last problem we’d define \(u\) to be one of the equations and \(v\) to be the other. Let’s do that real quick and see what we get.
Which equation we use to define \(u\) and \(v\) technically doesn’t matter. However, keep in mind that we’re eventually going to have to solve the resulting set of equations for \(x\) and \(y\) so let’s pick definitions with that in mind.
Let’s use the following definitions of \(u\) and \(v\) to get our transformation.
\[u = y - 4x\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}v = y\]The second definition is really just renaming \(y\) as \(v\). This isn’t a problem and in fact will make the rest of the problem a little easier. Note as well that all were really saying here is that the bottom side of the triangle won’t change under this transformation.
Okay, let’s think a little bit about what we have here. This will transform \(y - 4x = - 4\) into \(u = - 4\) and \(y = 0\) into \(v = 0\). These two side will form the right angle of the resulting triangle (which will occur where they intersect) and \(y + \frac{8}{3}x = 16\) will transform into the hypotenuse of this new triangle. If you aren’t sure you believe that then you should actually go through the work to verify it.
So, assuming you either believe us or have done the work to verify that what we’ve said is true we now have an issue that needs to be addressed.
The problem statement said that the right angle should occur at the origin. Under this transformation however the right angle will occur at \(\left( { - 4,0} \right)\) which means this isn’t the transformation we were asked to find unfortunately.
Note that we’re not saying that this isn’t a valid transformation. It absolutely is a valid, and not a particularly bad, transformation. It simply isn’t the transformation we were asked to find and so we can’t use it for this problem.
Fixing it however isn’t hard and if you really followed how we set this up you might see how to quickly “fix” things up.
Show Step 4So, we’ve decided that the definition of \(u\) and \(v\) we got in the last step isn’t the one we want for this problem so we need to fix things up a little bit.
The problem with our definition in the previous step was really that our definition of \(u\) transformed \(y - 4x = - 4\) into \(u = - 4\) and in order for the right angle to be at the origin we really need to have a side transform into \(u = 0\). Note our definition of \(v\) is already giving us a side with equation \(v = 0\) so we don’t need to worry about that one.
So, to fix this let’s write the first equation as follows,
\[y - 4x + 4 = 0\]Seems like a simple enough thing to do here. We simply added 4 to both sides to turn the right side into a zero. With this rewrite we can now see that in order to get a side to transform into the equation \(u = 0\) all we need to do is define \(u\) as follows,
\[u = y - 4x + 4\]This will transform the first equation into \(u = 0\) as we need and if we keep our definition of \(v\) as \(v = y\) the third equation will still transform into \(v = 0\) and so the right angle of the new triangle will now be at the origin and the hypotenuse of the new triangle will come from the applying the transformation to the third equation.
Show Step 5We now have our definitions of \(u\) and \(v\), given below for reference purposes, so all we need to do is solve the system of equation for \(x\) and \(y\).
\[\begin{align*}u & = y - 4x + 4\\ v & = y\end{align*}\]In this case, solving for \(x\) and \(y\) is really simple. We already know that \(y = v\) and so from the first equation we get,
\[u = v - 4x + 4\,\hspace{0.25in}\to \hspace{0.25in}\,\,\,x = \frac{1}{4}\left( {v - u + 4} \right)\]So, it looks like our transformation will be,
\[\begin{align*}x & = \frac{1}{4}\left( {v - u + 4} \right)\\ y & = v\end{align*}\] Show Step 6Now, technically we’ve done what the problem asked us to do. However, it probably wouldn’t be a bad thing to verify all the claims we made above by actually applying this transformation to the three equations and making sure we do get a right triangle with the right angle at the origin as we claimed.
Theoretically we wouldn’t need to apply the transformation to the first and third equation since we used those to define \(u\) and \(v\) that in turn gave us our transformation. However, it wouldn’t be a bad idea to apply the transformation to them to verify that we get what we expect to get. If we don’t then that would mean we probably made a mistake in the previous step.
So, here is the transformation applied to the three equations.
\(\displaystyle y = 4x - 4 :\hspace{0.25in}\,\,\,\,\,\,v = 4\left( {\frac{1}{4}} \right)\left( {v - u + 4} \right) - 4\,\,\,\,\,\,\hspace{0.25in}\to \hspace{0.25in}\,u = 0\)\(\displaystyle y = - \frac{8}{3}x + 16 :\hspace{0.25in}v = - \frac{8}{3}\left( {\frac{1}{4}} \right)\left( {v - u + 4} \right) + 16\hspace{0.25in}\to \hspace{0.25in}\,v = \frac{2}{5}u + 8\)
\(y = 0 :\hspace{0.5in}\,v = 0\)
Okay, so the first and third equations transformed as expected. Adding in the third equation and we get the following region.
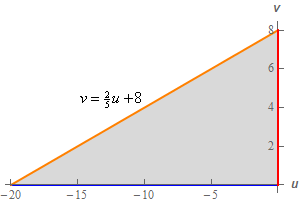
So, the resulting region is what we expected it to be. A right triangle with the right angle occurring at the origin.
Note however, that we did get something (maybe) unexpected here. The original triangle was completely in the 1st quadrant and the “new” triangle is completely in the 2nd quadrant. This kind of thing can happen with these types of problems so don’t worry about it when it does.
We got a triangle in the 2nd quadrant there because all the \(u\)’s ended up being negative. This suggests that maybe if we’d defined \(u\) to be \(u = - \left( {y - 4x + 4} \right) = - y + 4x - 4\) we might get a triangle in the 1st quadrant instead.
This isn’t guaranteed to work in general, but it does work this time. You might want to go through and verify this if you want the practice.