Calculus III - Change of Variables

Show General Notice Show Mobile Notice Show All Notes Hide All Notes

General Notice

I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.

Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.

Paul
February 18, 2026

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 15.8 : Change of Variables

Back to Problem List

5. If \(R\) is the parallelogram with vertices \(\left( {1,0} \right)\), \(\left( {4,3} \right)\), \(\left( {1,6} \right)\) and \(\left( { - 2,3} \right)\) determine the region we would get applying the transformation \(x = \frac{1}{2}\left( {v - u} \right)\), \(y = \frac{1}{2}\left( {v + u} \right)\) to \(R\).

Show All Steps Hide All Steps

Start Solution

Let’s start off with a sketch of \(R\).

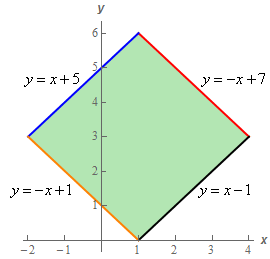
The equations of each of the boundaries of the region are given in the sketch. Given that we know the coordinates of each of the vertices its simple algebra to determine the equation of a line given two points on the line so we’ll leave it to you to verify the equations.

Show Step 2

Okay, now all we need to do is apply the transformation to each of the boundary equations. To do this we simply plug the transformation into each of the boundary equations.

Let’s start with \(y = x + 5\). Applying the transformation to this equation gives,

\[\begin{align*}\frac{1}{2}\left( {v + u} \right) & = \frac{1}{2}\left( {v - u} \right) + 5\\ v + u & = v - u + 10\\ 2u &= 10\hspace{0.5in} \Rightarrow \hspace{0.5in}\underline {u = 5} \end{align*}\]

So, this boundary will transform into the equation \(u = 5\).

Show Step 3

Let’s now apply the transformation to \(y = - x + 7\).

\[\begin{align*}\frac{1}{2}\left( {v + u} \right) & = - \frac{1}{2}\left( {v - u} \right) + 7\\ v + u & = - v + u + 14\\ 2v & = 14\hspace{0.5in} \Rightarrow \hspace{0.5in}\underline {v = 7} \end{align*}\]

This boundary transforms in the equation \(v = 7\).

Show Step 4

Next, let’s apply the transformation to \(y = x - 1\).

\[\begin{align*}\frac{1}{2}\left( {v + u} \right) & = \frac{1}{2}\left( {v - u} \right) - 1\\ v + u & = v - u - 2\\ 2u & = - 2\hspace{0.5in} \Rightarrow \hspace{0.5in}\underline {u = - 1} \end{align*}\]

So, this boundary will transform into the equation \(u = - 1\).

Show Step 5

Finally let’s apply the transformation to \(y = - x + 1\).

\[\begin{align*}\frac{1}{2}\left( {v + u} \right) & = - \frac{1}{2}\left( {v - u} \right) + 1\\ v + u & = - v + u + 2\\ 2v & = 2\hspace{0.5in} \Rightarrow \hspace{0.5in}\underline {v = 1} \end{align*}\]

This boundary transforms in the equation \(v = 1\).

Show Step 6

Sketching the transformed equations gives the following region.

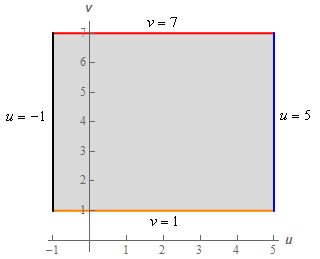
So, we transform the diamond shaped region into a rectangle under the transformation.

Note that we chose \(u\) to be the horizontal axis and \(v\) to be vertical axis in the transformed region for this problem. There is no real reason for doing that other than it is just what we’ve always done. Regardless of your choices here make sure to label the axes to make it clear!