I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 15.8 : Change of Variables
6. If \(R\) is the region bounded by \(xy = 1\), \(xy = 3\), \(y = 2\) and \(y = 6\) determine the region we would get applying the transformation \(\displaystyle x = \frac{v}{{6u}}\), \(y = 2u\) to \(R\).
Show All Steps Hide All Steps
Start SolutionLet’s start off with a sketch of \(R\).
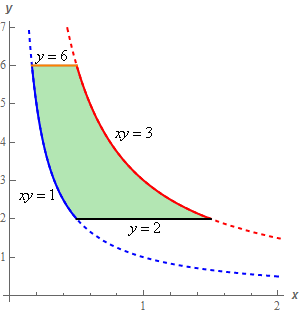
The equations of each of the boundaries of the region are given in the sketch. We also included “extensions” of the two curves (the dotted portions) just to show a fuller sketch of the two curves.
Show Step 2Okay, now all we need to do is apply the transformation to each of the boundary equations. To do this we simply plug the transformation into each of the boundary equations.
Let’s start with \(y = 6\). Applying the transformation to this equation gives,
\[2u = 6\hspace{0.5in} \Rightarrow \hspace{0.5in}\underline {u = 3} \]So, this boundary will transform into the equation \(u = 3\).
Show Step 3Let’s now apply the transformation to \(xy = 3\).
\[\begin{align*}\left( {\frac{v}{{6u}}} \right)\left( {2u} \right) & = 3\\ \frac{v}{3} & = 3\hspace{0.5in} \Rightarrow \hspace{0.5in}\underline {v = 9} \end{align*}\]This boundary transforms in the equation \(v = 9\).
Show Step 4Next, let’s apply the transformation to \(y = 2\).
\[2u = 2\hspace{0.5in} \Rightarrow \hspace{0.5in}\underline {u = 1} \]So, this boundary will transform into the equation \(u = 1\).
Show Step 5Finally let’s apply the transformation to \(xy = 1\).
\[\begin{align*}\left( {\frac{v}{{6u}}} \right)\left( {2u} \right) & = 1\\ \frac{v}{3} & = 1\hspace{0.5in} \Rightarrow \hspace{0.5in}\underline {v = 3} \end{align*}\]This boundary transforms in the equation \(v = 3\).
Show Step 6Sketching the transformed equations gives the following region.
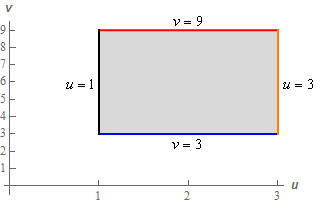
So, we transform the odd shaped region into a rectangle under the transformation.
Note that we chose \(u\) to be the horizontal axis and \(v\) to be vertical axis in the transformed region for this problem. There is no real reason for doing that other than it is just what we’ve always done. Regardless of your choices here make sure to label the axes to make it clear!