Section 15.8 : Change of Variables
7. Evaluate \(\displaystyle \iint\limits_{R}{{x{y^3}\,dA}}\) where \(R\) is the region bounded by \(xy = 1\), \(xy = 3\), \(y = 2\) and \(y = 6\) using the transformation \(\displaystyle x = \frac{v}{{6u}}\), \(y = 2u\).
Show All Steps Hide All Steps
Start SolutionThe first thing we need to do is determine the transformation of \(R\). We actually determined the transformation of \(R\) in the previous example. However, let’s go through the process again (with a few details omitted) just to have it here in this problem.
First, a sketch of \(R\).
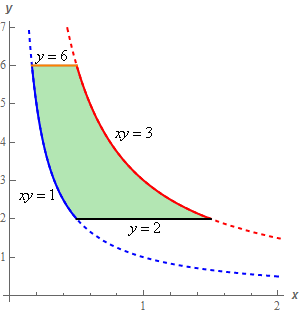
Now, let’s transform each of the boundary curves.
\(y = 6:\hspace{0.25in}2u = 6\hspace{0.5in} \to \hspace{0.25in}\,\,\,u = 3\)\(\displaystyle xy = 3:\,\,\,\,\,\,\,\,\,\left( {\frac{v}{{6u}}} \right)\left( {2u} \right) = 3\,\hspace{0.25in}\to \hspace{0.25in}\,\,\,v = 9\)
\(y = 2:\hspace{0.25in}2u = 2\hspace{0.5in} \to \hspace{0.25in}\,\,\,u = 1\)
\(\displaystyle xy = 1:\,\,\,\,\,\,\,\,\,\left( {\frac{v}{{6u}}} \right)\left( {2u} \right) = 1\,\,\hspace{0.25in}\to \hspace{0.25in}\,\,\,v = 3\)
Here is a sketch of the transformed region.
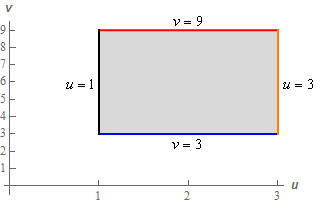
So, the limits for the transformed region are,
\[\begin{array}{c}1 \le u \le 3\\ 3 \le v \le 9\end{array}\] Show Step 2We’ll need the Jacobian of this transformation next.
\[\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}} = \left| {\begin{array}{*{20}{c}}{\displaystyle \frac{{\partial x}}{{\partial u}}}&\displaystyle {\frac{{\partial x}}{{\partial v}}}\\\displaystyle {\frac{{\partial y}}{{\partial u}}}&\displaystyle {\frac{{\partial y}}{{\partial v}}}\end{array}} \right| = \left| {\begin{array}{*{20}{c}}{\displaystyle - \frac{v}{{6{u^2}}}}&{\displaystyle \frac{1}{{6u}}}\\ & \\2&0\end{array}} \right| = 0 - \frac{2}{{6u}} = - \frac{1}{{3u}}\] Show Step 3We can now write the integral in terms of the “new” \(uv\) coordinates system.
\[\begin{align*}\iint\limits_{R}{{x{y^3}\,dA}} & = \int_{1}^{3}{{\int_{3}^{9}{{\left( {\frac{v}{{6u}}} \right){{\left( {2u} \right)}^3}\left| { - \frac{1}{{3u}}} \right|\,dv}}\,du}}\\ & = \int_{1}^{3}{{\int_{3}^{9}{{\frac{4}{9}v\,u\,dv}}\,du}}\end{align*}\]Don’t forget to add in the Jacobian and don’t forget that we need absolute value bars on it. In this case we know that the range of \(u\) we’re working on (given in Step 1) is positive we know that the quantity in the absolute value bars is negative and so we can drop the absolute value bars by also dropping the minus sign.
Also, the simplified integrand didn’t suggest any one order of integration over the other and so we just chose one to work with. The other order would be just as easy to have worked with.
Show Step 4Finally, let’s evaluate the integral.
\[\begin{align*}\iint\limits_{R}{{x{y^3}\,dA}} & = \int_{1}^{3}{{\int_{3}^{9}{{\frac{4}{9}v\,u\,dv}}\,du}}\\ & = \int_{1}^{3}{{\left. {\left( {\frac{2}{9}{v^2}u} \right)} \right|_3^9\,du}}\\ & = \int_{1}^{3}{{16u\,du}}\\ & = \left. {\left( {8{u^2}} \right)} \right|_1^3\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{64}}\end{align*}\]