Section 15.3 : Double Integrals over General Regions
1. Evaluate\( \displaystyle \iint\limits_{D}{{42{y^2} - 12x\,dA}}\) where \(D = \left\{ {\left( {x,y} \right)|0 \le x \le 4,{{\left( {x - 2} \right)}^2} \le y \le 6} \right\}\)
Show All Steps Hide All Steps
Start SolutionBelow is a quick sketch of the region \(D\).
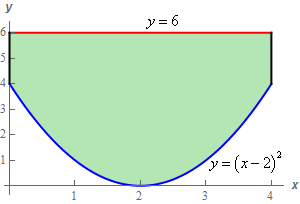
In general, this sketch is often important to setting the integral up correctly. We’ll need to determine the order of integration and often the region will “force” a particular order. Many regions can only be dealt with easily by doing one particular order of integration and sometimes the only way to really see that is to have a sketch of \(D\).
Even if you can do the integral in either order the sketch of \(D\) will often help with setting up the limits for the integrals.
Show Step 2With this problem we were pretty much given the order of integration by how the region \(D\) was specified in the problem statement. Note however, that the sketch shows that this was pretty much the only easy order of integration. The same function is always on the top of the region and the same function is always on the bottom of the region and so it makes sense to integrate \(y\) first.
If we wanted to integrate \(x\) first we’d have a messier integration to deal with. First the right/left functions change and so we couldn’t do the \(x\) integration with a single integral. The \(x\) integration would require two integrals in this case. There is also the fact that the lower portion of the region has the same function for both the right and left sides. The equation could be solved for \(x\), as we’d need to in order to \(x\) integration first, and often that is either very difficult or would give unpleasant limits. It wouldn’t be too difficult in this case but it would put roots into the limits and that often makes for messier integration.
So, let’s go with the order of integration specified in the problem statement and because we were given \(D\) in the set builder notation we also were given the limits for both \(x\) and \(y\) which is nice as we usually will need to figure those out on our own.
Here is the integral set up for \(y\) integration first.
\[\iint\limits_{D}{{42{y^2} - 12x\,dA}} = \int_{0}^{4}{{\int_{{{{\left( {x - 2} \right)}^2}}}^{6}{{42{y^2} - 12x\,dy}}\,dx}}\] Show Step 3Here is the \(y\) integration.
\[\begin{align*}\iint\limits_{D}{{42{y^2} - 12x\,dA}} & = \int_{0}^{4}{{\int_{{{{\left( {x - 2} \right)}^2}}}^{6}{{42{y^2} - 12x\,dy}}\,dx}}\\ & = \int_{0}^{4}{{\left. {\left( {14{y^3} - 12xy} \right)} \right|_{{{\left( {x - 2} \right)}^2}}^6\,dx}}\\ & = \int_{0}^{4}{{3024 - 72x - 14{{\left( {x - 2} \right)}^6} + 12x{{\left( {x - 2} \right)}^2}\,dx}}\end{align*}\] Show Step 4Now, we did not do any real simplification of the integrand in the last step. There was a reason for that.
After doing the first integration students will often just launch into a “simplification” mode and multiply everything out and “simplify” everything. Sometimes that does need to be done and we don’t want to give the impression it is never a good thing or never needs to be done.
However, take a look at the third term above. It could be multiplied out if we wanted to but it would take a little bit of time and there is a chance we’d mess up a sign or coefficient somewhere. We are going to be integrating and the third term can be integrated very quickly with a simple Calculus I substitution. In other words, why bother with the messy multiplication with that term when it does not need to be done.
The fourth term, on the other hand, does need to be multiplied out because of the extra \(x\) that is in the front of the term.
So, before just launching into “simplification” mode take a quick look at the integrand and see if there are any terms that can be done with a simple substitution as we won’t need to mess with those terms. Only multiply out terms that actually need to be multiplied out.
Here is the \(x\) integration work. We will leave the Algebra details to you to verify and we’ll also be leaving the Calculus I substitution work to you to verify.
\[\begin{align*}\iint\limits_{D}{{42{y^2} - 12x\,dA}} & = \int_{0}^{4}{{3024 - 72x - 14{{\left( {x - 2} \right)}^6} + 12x{{\left( {x - 2} \right)}^2}\,dx}}\\ & = \int_{0}^{4}{{3024 - 24x - 48{x^2} + 12{x^3} - 14{{\left( {x - 2} \right)}^6}\,dx}}\\ & = \left. {\left( {3024x - 12{x^2} - 16{x^3} + 3{x^4} - 2{{\left( {x - 2} \right)}^7}} \right)} \right|_0^4 = \require{bbox} \bbox[2pt,border:1px solid black]{{11136}}\end{align*}\]Before leaving this problem let’s again note how much easier dealing with the third term was because we did not multiply it out and just used a substitution. Made this problem a lot easier.
Also note that this problem illustrated an important point that needs to be made with many of these integrals. These integrals will often get very messy after the first integration. You need to be ready for that and expect it to happen on occasion. Just because they start off looking “easy” doesn’t mean that they will remain easy throughout the whole problem. Just because it becomes a mess doesn’t mean you’ve made a mistake, although that is unfortunately always a possible reason for a messy integral. It may just mean this is one of those integrals that get somewhat messy before they are done.