Section 15.3 : Double Integrals over General Regions
4. Evaluate \( \displaystyle \iint\limits_{D}{{x\left( {y - 1} \right)\,dA}}\) where \(D\) is the region bounded by \(y = 1 - {x^2}\) and \(y = {x^2} - 3\).
Show All Steps Hide All Steps
Start SolutionBelow is a quick sketch of the region \(D\).
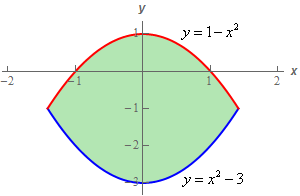
In general, this sketch is often important to setting the integral up correctly. We’ll need to determine the order of integration and often the region will “force” a particular order. Many regions can only be dealt with easily by doing one particular order of integration and sometimes the only way to really see that is to have a sketch of \(D\).
Even if you can do the integral in either order the sketch of \(D\) will often help with setting up the limits for the integrals.
Show Step 2With this problem the region is really only set up to integrate \(y\) first. Integrating \(x\) first would require two integrals (the right/left functions change) and the limits for the \(x\)’s would be a little messy to deal with.
So, here are the limits for this integral.
\[\begin{array}{c} - \sqrt 2 \le x \le \sqrt 2 \\ {x^2} - 3 \le y \le 1 - {x^2}\end{array}\]The \(x\) limits can easily be found by setting the two equations equal and solving for \(x\).
Show Step 3Here is the integral set up for \(y\) integration first.
\[\iint\limits_{D}{{x\left( {y - 1} \right)\,dA}} = \int_{{ - \sqrt 2 }}^{{\sqrt 2 }}{{\int_{{{x^2} - 3}}^{{1 - {x^2}}}{{x\left( {y - 1} \right)\,dy}}\,dx}}\] Show Step 4Here is the \(y\) integration.
\[\begin{align*}\iint\limits_{D}{{x\left( {y - 1} \right)\,dA}} & = \int_{{ - \sqrt 2 }}^{{\sqrt 2 }}{{\int_{{{x^2} - 3}}^{{1 - {x^2}}}{{x\left( {y - 1} \right)\,dy}}\,dx}}\\ & = \int_{{ - \sqrt 2 }}^{{\sqrt 2 }}{{\left. {\left( {x\left( {\frac{1}{2}{y^2} - y} \right)} \right)} \right|_{{x^2} - 3}^{1 - {x^2}}\,dx}}\\ & = \int_{{ - \sqrt 2 }}^{{\sqrt 2 }}{{\frac{1}{2}x{{\left( {1 - {x^2}} \right)}^2} - \frac{1}{2}x{{\left( {{x^2} - 3} \right)}^2} - x\left( {1 - {x^2}} \right) + x\left( {{x^2} - 3} \right)\,dx}}\end{align*}\] Show Step 5With this problem we have two options in dealing with the simplification of the integrand. The 3rd and 4th terms will need to be simplified. The 1st and 2nd terms however can be simplified, and they aren’t that hard to simplify or we could do a fairly quick Calculus I substitutions for each of them.
If you multiply everything out you will get the following integral.
\[\iint\limits_{D}{{x\left( {y - 1} \right)\,dA}} = \int_{{ - \sqrt 2 }}^{{\sqrt 2 }}{{4{x^3} - 8x\,dx}} = \left. {\left( {{x^4} - 4{x^2}} \right)} \right|_{ - \sqrt 2 }^{\sqrt 2 } = \require{bbox} \bbox[2pt,border:1px solid black]{0}\]There is a lot of cancelation going on with this integrand. It isn’t obvious however that there would be that much cancelling at first glance and the multiplication required to do the cancelling is the type where it is easy to miss a minus sign and get the wrong integrand and then a wrong answer.
So, let’s also do the substitution path to see the difference. Doing that gives,
\[\begin{align*}\iint\limits_{D}{{x\left( {y - 1} \right)\,dA}} & = \int_{{ - \sqrt 2 }}^{{\sqrt 2 }}{{\frac{1}{2}x{{\left( {1 - {x^2}} \right)}^2} - \frac{1}{2}x{{\left( {{x^2} - 3} \right)}^2} + 2{x^3} - 4x\,dx}}\\ & = \left. {\left( { - \frac{1}{{12}}{{\left( {1 - {x^2}} \right)}^3} - \frac{1}{{12}}{{\left( {{x^2} - 3} \right)}^3} + \frac{1}{2}{x^4} - 2{x^2}} \right)} \right|_{ - \sqrt 2 }^{\sqrt 2 } = \require{bbox} \bbox[2pt,border:1px solid black]{0}\end{align*}\]So, the same answer which shouldn’t be very surprising, but a slightly messier integration and evaluation process. Which path you chose to take and which path you feel is the easier of the two is probably very dependent on the person. As shown however you will get the same answer so you won’t need to worry about that.