Section 16.2 : Line Integrals - Part I
1. Evaluate \(\displaystyle \int\limits_{C}{{3{x^2} - 2y\,ds}}\) where \(C\) is the line segment from \(\left( {3,6} \right)\) to \(\left( {1, - 1} \right)\).
Show All Steps Hide All Steps
Start SolutionHere is a quick sketch of \(C\) with the direction specified in the problem statement shown.
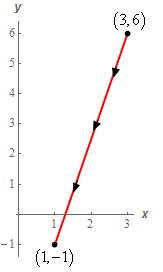
Now, with the specified direction we can see that \(x\) is decreasing as we move along the curve in the specified direction. This means that we can’t just determine the equation of the line and use that to work the problem. Using the equation of the line would require us to use increasing \(x\) since the limits in the integral must go from smaller to larger value.
We could of course use the fact from the notes that relates the line integral with a specified direction and the line integral with the opposite direction to allow us to use the equation of the line. However, for this problem let’s just work with problem without the fact to make sure we can do that type of problem
So, we’ll need to parameterize this line and we know how to parameterize the equation of a line between two points. Here is the vector form of the parameterization of the line.
\[\vec r\left( t \right) = \left( {1 - t} \right)\left\langle {3,6} \right\rangle + t\left\langle {1, - 1} \right\rangle = \left\langle {3 - 2t,6 - 7t} \right\rangle \,\,\,\,\,\,\,\,0 \le t \le 1\]We could also break this up into parameter form as follows.
\[\begin{array}{*{20}{l}}{x = 3 - 2t}\\{y = 6 - 7t}\end{array}\hspace{0.25in}0 \le t \le 1\]Either form of the parameterization will work for the problem but we’ll use the vector form for the rest of this problem.
Show Step 3We’ll need the magnitude of the derivative of the parameterization so let’s get that.
\[\vec r'\left( t \right) = \left\langle { - 2, - 7} \right\rangle \hspace{0.25in}\hspace{0.25in}\left\| {\vec r'\left( t \right)} \right\| = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 7} \right)}^2}} = \sqrt {53} \]We’ll also need the integrand “evaluated” at the parameterization. Recall all this means is we replace the \(x\)/\(y\) in the integrand with the \(x\)/\(y\) from parameterization. Here is the integrand evaluated at the parameterization.
\[3{x^2} - 2y = 3{\left( {3 - 2t} \right)^2} - 2\left( {6 - 7t} \right) = 3{\left( {3 - 2t} \right)^2} - 12 + 14t\] Show Step 4The line integral is then,
\[\begin{align*}\int\limits_{C}{{3{x^2} - 2y\,ds}} & = \int_{0}^{1}{{\left( {3{{\left( {3 - 2t} \right)}^2} - 12 + 14t} \right)\sqrt {53} \,dt}}\\ & = \sqrt {53} \left. {\left[ { - \frac{1}{2}{{\left( {3 - 2t} \right)}^3} - 12t + 7{t^2}} \right]} \right|_0^1 = \require{bbox} \bbox[2pt,border:1px solid black]{{8\sqrt {53} }}\end{align*}\]Note that we didn’t multiply out the first term in the integrand as we could do a quick substitution to do the integral.