Section 16.2 : Line Integrals - Part I
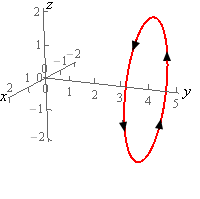
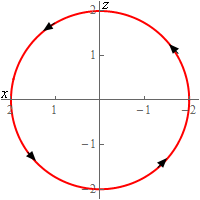
5. Evaluate \( \displaystyle \int\limits_{C}{{{x^2}{y^2}\,ds}}\) where \(C\) is the circle centered at the origin of radius 2 centered on the \(y\)-axis at \(y = 4\). See the sketches below for orientation. Note the “odd” axis orientation on the 2D circle is intentionally that way to match the 3D axis the direction.
Show All Steps Hide All Steps
Start SolutionBefore we parameterize the curve note that the “orientation” of the \(x\)-axis in the 2D sketch above is backwards from what we are used to. In this sketch the positive \(x\)-axis is to the left and the negative \(x\)-axis is to the right. This was done to match up with the 3D image.
If we were on the positive \(y\)-axis (on the 3D image of course) past \(y = 4\) and looking towards the origin we would see the 2D sketch. Generating the 2D sketch in this manner will help to make sure that our parameterization has the correct direction.
Speaking of which, here is the parameterization of the curve.
\[\vec r\left( t \right) = \left\langle {2\cos \left( t \right),4, - 2\sin \left( t \right)} \right\rangle \,\,\,\,\,\,\,\,0 \le t \le 2\pi \]If you check the parameterization at \(t = 0,\frac{\pi }{2},\pi ,\frac{{3\pi }}{2}\) we can see that we will get the correct \(\left( {x,z} \right)\) coordinates for the curve in the 2D sketch and hence we will also get the correct coordinates for the curve in the 3D sketch.
Don’t forget that we also need to acknowledge in our parameterization that we are at \(y = 4\), i.e. the second component of the parameterization. When one of the coordinates on a 3D curve is constant it is often easy to forget to deal with it in the parameterization.
Show Step 2We’ll need the magnitude of the derivative of the parameterization so let’s get that.
\[\begin{align*}\vec r'\left( t \right) & = \left\langle { - 2\sin \left( t \right),0, - 2\cos \left( t \right)} \right\rangle \\ \left\| {\vec r'\left( t \right)} \right\| & = \sqrt {{{\left( { - 2\sin \left( t \right)} \right)}^2} + {{\left( 0 \right)}^2} + {{\left( { - 2\cos \left( t \right)} \right)}^2}} \\ & = \sqrt {4{{\sin }^2}\left( t \right) + 4{{\cos }^2}\left( t \right)} = \sqrt {4\left( {{{\sin }^2}\left( t \right) + {{\cos }^2}\left( t \right)} \right)} = \sqrt 4 = 2\end{align*}\]We’ll also need the integrand “evaluated” at the parameterization. Recall all this means is we replace the \(x\)/y/z in the integrand with the \(x\)/y/z from parameterization. Here is the integrand evaluated at the parameterization.
\[{x^2}{y^2} = {\left( {2\cos \left( t \right)} \right)^2}{\left( 4 \right)^2} = 64{\cos ^2}\left( t \right)\] Show Step 3The line integral is then,
\[\begin{align*}\int\limits_{C}{{{x^2}{y^2}\,ds}} & = \int_{0}^{{2\pi }}{{\left( {64{{\cos }^2}\left( t \right)} \right)\left( 2 \right)\,dt}} = \int_{0}^{{2\pi }}{{64\left( {1 + \cos \left( {2t} \right)} \right)\,dt}}\\ & = \left. {64\left( {t + \frac{1}{2}\sin \left( {2t} \right)} \right)} \right|_0^{2\pi } = \require{bbox} \bbox[2pt,border:1px solid black]{{128\pi }}\end{align*}\]You do recall how to use the double angle formula for cosine to evaluate this integral correct? We’ll be seeing a fair number of integrals involving trig functions in this chapter and knowing how to do these kinds of integrals will be important.