Section 16.2 : Line Integrals - Part I
7. Evaluate \( \displaystyle \int\limits_{C}{{4y - x\,ds}}\) where \(C\) is the upper portion of the circle centered at the origin of radius 3 from \(\displaystyle\left( {\frac{3}{{\sqrt 2 }},\frac{3}{{\sqrt 2 }}} \right)\) to \(\displaystyle\left( { - \frac{3}{{\sqrt 2 }}, - \frac{3}{{\sqrt 2 }}} \right)\) in the counter clockwise rotation followed by the line segment from \(\displaystyle\left( { - \frac{3}{{\sqrt 2 }}, - \frac{3}{{\sqrt 2 }}} \right)\) to \(\displaystyle\left( {4, - \frac{3}{{\sqrt 2 }}} \right)\) which in turn is followed by the line segment from \(\displaystyle\left( {4, - \frac{3}{{\sqrt 2 }}} \right)\) to \(\left( {4,4} \right)\). See the sketch below for the direction.

Show All Steps Hide All Steps
Start SolutionTo help with the problem let’s label each of the curves as follows,
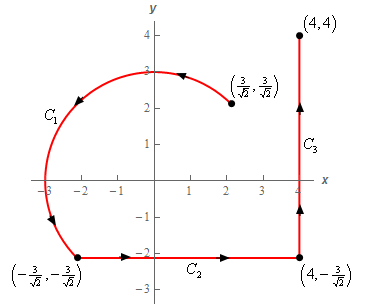
Now let’s parameterize each of these curves.
\(\displaystyle {C_1}:\,\,\vec r\left( t \right) = \left\langle {3\cos \left( t \right),3\sin \left( t \right)} \right\rangle \hspace{0.25in}\,\,\,\,\,\,\,\frac{1}{4}\pi \le t \le \frac{5}{4}\pi \)\(\displaystyle {C_2}:\,\,\vec r\left( t \right) = \left\langle {t, - \frac{3}{{\sqrt 2 }}} \right\rangle \hspace{0.25in} - \frac{3}{{\sqrt 2 }} \le t \le 4\)
\(\displaystyle {C_3}:\,\,\vec r\left( t \right) = \left\langle {4,t} \right\rangle \hspace{0.25in} - \frac{3}{{\sqrt 2 }} \le t \le 4\)
The limits for \({C_1}\) are actually pretty easy to find. At the starting point, \(\left( {\frac{3}{{\sqrt 2 }},\frac{3}{{\sqrt 2 }}} \right)\), we know that we must have,
\[3\cos \left( t \right) = 3\sin \left( t \right) = \frac{3}{{\sqrt 2 }}\,\,\,\,\,\,\,\,\,\,\,\,\, \to \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\cos \left( t \right) = \sin \left( t \right) = \frac{1}{{\sqrt 2 }}\,\,\,\,\,\,\,\,\,\,\, \to \,\,\,\,\,\,\,\,\,\tan \left( t \right) = 1\]Since the starting point of \({C_1}\) is in the 1st quadrant we know that we must have \(t = \frac{1}{4}\pi \).
We can do a similar argument of the final point, \(\left( { - \frac{3}{{\sqrt 2 }}, - \frac{3}{{\sqrt 2 }}} \right)\). This point is in the 3rd quadrant and again we’ll have \(\tan \left( t \right) = 1\). Therefore we must have \(t = \frac{5}{4}\pi \) at this point.
For \({C_2}\) and \({C_3}\) we just used the equations of the lines since they were horizontal and vertical respectively and followed increasing \(x\) and \(y\) respectively. The limits for them are a little unpleasant but we can’t do anything about the fact that there will be messy numbers in these no matter how we do them.
Show Step 2Okay, we now need to compute the line integral along each of these curves. Unlike the first few problems in this section where we found the magnitude and the integrand prior to the integration step we’re just going to just straight into the integral and do all the work there.
Here is the integral along each of the curves.
\[\begin{align*}\int\limits_{{{C_1}}}{{4y - x\,ds}} &= \int_{{\frac{1}{4}\pi }}^{{\frac{5}{4}\pi }}{{\left[ {4\left( {3\sin \left( t \right)} \right) - 3\cos \left( t \right)} \right]\sqrt {{{\left( { - 3\sin \left( t \right)} \right)}^2} + {{\left( {3\cos \left( t \right)} \right)}^2}} \,dt}}\\ & = \int_{{\frac{1}{4}\pi }}^{{\frac{5}{4}\pi }}{{\left[ {12\sin \left( t \right) - 3\cos \left( t \right)} \right]\sqrt {9{{\sin }^2}\left( t \right) + 9{{\cos }^2}\left( t \right)} \,dt}}\\ & = 3\int_{{\frac{1}{4}\pi }}^{{\frac{5}{4}\pi }}{{12\sin \left( t \right) - 3\cos \left( t \right)\,dt}}\\ & = \left. {3\left( { - 12\cos \left( t \right) - 3\sin \left( t \right)} \right)} \right|_{\frac{1}{4}\pi }^{\frac{5}{4}\pi } = \underline {\frac{{90}}{{\sqrt 2 }}} \end{align*}\] \[\begin{align*}\int\limits_{{{C_2}}}{{4y - x\,ds}} &= \int_{{ - \,\,\frac{3}{{\sqrt 2 }}}}^{4}{{\left[ {4\left( { - \frac{3}{{\sqrt 2 }}} \right) - t} \right]\sqrt {{{\left( 1 \right)}^2} + {{\left( 0 \right)}^2}} \,dt}}\\ & = \int_{{ - \,\,\frac{3}{{\sqrt 2 }}}}^{4}{{ - \frac{{12}}{{\sqrt 2 }} - t\,dt}}\\ & = \left. {\left( { - \frac{{12}}{{\sqrt 2 }}t - \frac{1}{2}{t^2}} \right)} \right|_{ - \,\,\frac{3}{{\sqrt 2 }}}^4 = \underline { - \frac{{95}}{4} - \frac{{48}}{{\sqrt 2 }}} \end{align*}\] \[\begin{align*}\int\limits_{{{C_3}}}{{4y - x\,ds}} &= \int_{{ - \,\,\frac{3}{{\sqrt 2 }}}}^{4}{{\left[ {4\left( t \right) - 4} \right]\sqrt {{{\left( 0 \right)}^2} + {{\left( 1 \right)}^2}} \,dt}}\\ & = \int_{{ - \,\,\frac{3}{{\sqrt 2 }}}}^{4}{{4t - 4\,dt}}\\ & = \left. {\left( {2{t^2} - 4t} \right)} \right|_{ - \,\,\frac{3}{{\sqrt 2 }}}^4 = \require{bbox} \bbox[2pt,border:1px solid black]{{7 - \frac{{12}}{{\sqrt 2 }}}}\end{align*}\] Show Step 3Okay to finish this problem out all we need to do is add up the line integrals over these curves to get the full line integral.
\[\int\limits_{C}{{4y - x\,ds}} = \left( {\frac{{90}}{{\sqrt 2 }}} \right) + \left( { - \frac{{95}}{4} - \frac{{48}}{{\sqrt 2 }}} \right) + \left( {7 - \frac{{12}}{{\sqrt 2 }}} \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{ - \frac{{67}}{4} + \frac{{30}}{{\sqrt 2 }} = 4.4632}}\]Note that we put parenthesis around the result of each individual line integral simply to illustrate where it came from and they aren’t needed in general of course.