Section 16.2 : Line Integrals - Part I
9. Evaluate \( \displaystyle \int\limits_{C}{{4{x^2}\,ds}}\) for each of the following curves.
- \(C\) is the portion of the circle centered at the origin of radius 2 in the 1st quadrant rotating in the clockwise direction.
- \(C\) is the line segment from \(\left( {0,2} \right)\) to \(\left( {2,0} \right)\).
Start Solution
Let’s start off with a quick sketch of the curve for this part of the problem.
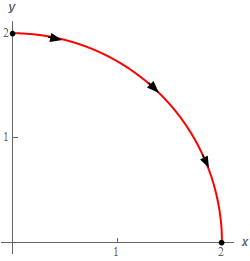
Here is the parameterization for this curve.
\(C:\,\,\vec r\left( t \right) = \left\langle {2\sin \left( t \right),2\cos \left( t \right)} \right\rangle \hspace{0.25in}\,\,\,\,\,\,\,0 \le t \le \frac{1}{2}\pi \)Show Step 2
Here is the line integral for this curve.
\[\begin{align*}\int\limits_{C}{{4{x^2}\,ds}} &= \int_{0}^{{\frac{1}{2}\pi }}{{4{{\left( {2\sin \left( t \right)} \right)}^2}\sqrt {{{\left( {2\cos \left( t \right)} \right)}^2} + {{\left( { - 2\sin \left( t \right)} \right)}^2}} \,dt}}\\ & = \int_{0}^{{\frac{1}{2}\pi }}{{16{{\sin }^2}\left( t \right)\sqrt {4{{\cos }^2}\left( t \right) + 4{{\sin }^2}\left( t \right)} \,dt}}\\ & = \int_{0}^{{\frac{1}{2}\pi }}{{16{{\sin }^2}\left( t \right)\sqrt 4 \,dt}}\\ & = \int_{0}^{{\frac{1}{2}\pi }}{{32\left( {\frac{1}{2}} \right)\left( {1 - \cos \left( {2t} \right)} \right)\,dt}}\\ & = \left. {16\left( {t - \frac{1}{2}\sin \left( {2t} \right)} \right)} \right|_0^{\frac{1}{2}\pi } = \require{bbox} \bbox[2pt,border:1px solid black]{{8\pi }}\end{align*}\]b \(C\) is the line segment from \(\left( {0,2} \right)\) to \(\left( {2,0} \right)\). Show All Steps Hide All Steps
Start Solution
Let’s start off with a quick sketch of the curve for this part of the problem.

So, what we have in this part is a different curve that goes from \(\left( {0,2} \right)\) to \(\left( {2,0} \right)\). Despite the fact that this curve has the same starting and ending point as the curve in the first part there is no reason to expect the line integral to have the same value. Therefore we’ll need to go through the work and see what we get from the line integral.
We’ll need to parameterize the curve so let’s take care of that.
\(C:\,\,\vec r\left( t \right) = \left( {1 - t} \right)\left\langle {0,2} \right\rangle + t\left\langle {2,0} \right\rangle = \left\langle {2t,2 - 2t} \right\rangle \hspace{0.25in}\,\,\,\,\,\,\,0 \le t \le 1\)Note that we could have just found the equation of this curve but it seemed just as easy to just use the vector form of the line segment between two points.
Show Step 2Now all we need to do is compute the line integral.
\[\begin{align*}\int\limits_{C}{{4{x^2}\,ds}} & = \int_{0}^{1}{{4{{\left( {2t} \right)}^2}\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 2} \right)}^2}} \,dt}}\\ & = \sqrt 8 \int_{0}^{1}{{16{t^2}\,dt}}\\ & = \left. {2\sqrt 2 \left( {\frac{{16}}{3}{t^3}} \right)} \right|_0^1 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{32\sqrt 2 }}{3}}}\end{align*}\]So, as noted at the start of this part the value of the line integral was not the same as the value of the line integral in the first part despite the same starting and ending points for the curve. Note that it is possible for two line integrals with the same starting and ending points to have the same value but we can’t expect that to happen and so need to go through and do the work.