Section 16.3 : Line Integrals - Part II
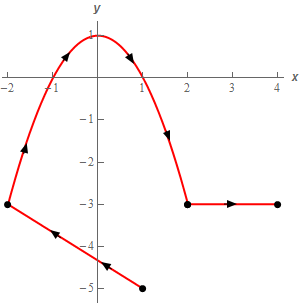
5. Evaluate \( \displaystyle \int\limits_{C}{{2{x^2}\,dy - xy\,dx}}\) where \(C\) is the line segment from \(\left( {1, - 5} \right)\) to \(\left( { - 2, - 3} \right)\) followed by the portion of \(y = 1 - {x^2}\) from \(x = - 2\) to \(x = 2\) which in turn is followed by the line segment from \(\left( {2, - 3} \right)\) to \(\left( {4, - 3} \right)\). See the sketch below for the direction.
Show All Steps Hide All Steps
Start SolutionTo help with the problem let’s label each of the curves as follows,
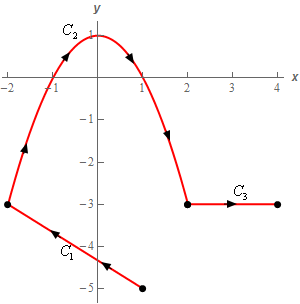
Now let’s parameterize each of these curves.
\({C_1}:\,\,\vec r\left( t \right) = \left( {1 - t} \right)\left\langle {1, - 5} \right\rangle + t\left\langle { - 2, - 3} \right\rangle = \left\langle {1 - 3t, - 5 + 2t} \right\rangle \hspace{0.25in}0 \le t \le 1\)\({C_2}:\,\,\vec r\left( t \right) = \left\langle {t,1 - {t^2}} \right\rangle \hspace{0.25in} - 2 \le t \le 2\)
\({C_3}:\,\,\vec r\left( t \right) = \left\langle {t, - 3} \right\rangle \hspace{0.25in}2 \le t \le 4\)
Note that for \({C_1}\) we had to use the vector form for the line segment between two points because the specified direction was in the decreasing \(x\) direction and so the equation of the line wouldn’t work since the limits of the line integral need to go from smaller to larger values.
We did just use the equation of the line for \({C_3}\) since it was simple enough to do and the limits were also nice enough.
Show Step 2Now we need to compute the line integral for each of the curves.
\[\begin{align*}\int\limits_{{{C_1}}}{{2{x^2}\,dy - xy\,dx}} &= \int\limits_{{{C_1}}}{{2{x^2}\,dy}} - \int\limits_{{{C_1}}}{{xy\,dx}}\\ & = \int_{0}^{1}{{2{{\left( {1 - 3t} \right)}^2}\left( 2 \right)\,dt}} - \int_{0}^{1}{{\left( {1 - 3t} \right)\left( { - 5 + 2t} \right)\left( { - 3} \right)\,dt}}\\ & = \int_{0}^{1}{{4{{\left( {1 - 3t} \right)}^2} - 3\left( {6{t^2} - 17t + 5} \right)\,dt}}\\ & = \left. {\left( { - \frac{4}{9}{{\left( {1 - 3t} \right)}^3} - 3\left( {2{t^3} - \frac{{17}}{2}{t^2} + 5t} \right)} \right)} \right|_0^1 = \underline {\frac{{17}}{2}} \end{align*}\] \[\begin{align*}\int\limits_{{{C_2}}}{{2{x^2}\,dy - xy\,dx}} &= \int\limits_{{{C_2}}}{{2{x^2}\,dy}} - \int\limits_{{{C_2}}}{{xy\,dx}}\\ & = \int_{{ - 2}}^{2}{{2{{\left( t \right)}^2}\left( { - 2t} \right)\,dt}} - \int_{{ - 2}}^{2}{{\left( t \right)\left( {1 - {t^2}} \right)\left( 1 \right)\,dt}}\\ & = \int_{{ - 2}}^{2}{{ - 3{t^3} - t\,dt}}\\ & = \left. {\left( { - \frac{3}{4}{t^4} - \frac{1}{2}{t^2}} \right)} \right|_{ - 2}^2 = \underline 0 \end{align*}\] \[\begin{align*}\int\limits_{{{C_3}}}{{2{x^2}\,dy - xy\,dx}} &= \int\limits_{{{C_3}}}{{2{x^2}\,dy}} - \int\limits_{{{C_2}}}{{xy\,dx}}\\ & = \int_{2}^{4}{{2{{\left( t \right)}^2}\left( 0 \right)\,dt}} - \int_{2}^{4}{{\left( t \right)\left( { - 3} \right)\left( 1 \right)\,dt}}\\ & = \int_{2}^{4}{{3t\,dt}}\\ & = \left. {\left( {\frac{3}{2}{t^2}} \right)} \right|_2^4 = \underline {18} \end{align*}\]Don’t forget to correctly deal with the differentials when converting the line integral into a “standard” integral.
Also, don’t get excited when one of the differentials “evaluates” to zero as the first one did in the \({C_3}\) integral. That will happen on occasion and is not something to get worried about when it does.
Show Step 3Okay to finish this problem out all we need to do is add up the line integrals over these curves to get the full line integral.
\[ \displaystyle \int\limits_{C}{{2{x^2}\,dy - xy\,dx}} = \left( {\frac{{17}}{2}} \right) + \left( 0 \right) + \left( {18} \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{53}}{2}}}\]Note that we put parenthesis around the result of each individual line integral simply to illustrate where it came from and they aren’t needed in general of course.