I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 16.4 : Line Integrals of Vector Fields
3. Evaluate \( \displaystyle \int\limits_{C}{{\vec F\centerdot d\vec r}}\) where \(\vec F\left( {x,y} \right) = {y^2}\,\vec i + \left( {{x^2} - 4} \right)\vec j\) and \(C\) is the portion of \(y = {\left( {x - 1} \right)^2}\) from \(x = 0\) to \(x = 3\).
Show All Steps Hide All Steps
Start SolutionHere is a quick sketch of \(C\) with the direction specified in the problem statement shown.
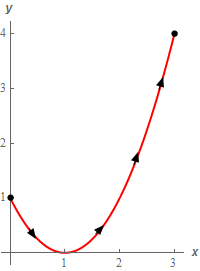
Next, we need to parameterize the curve.
\[\vec r\left( t \right) = \left\langle {t,{{\left( {t - 1} \right)}^2}} \right\rangle \,\,\,\,\,\,\,\,0 \le t \le 3\] Show Step 3In order to evaluate this line integral we’ll need the dot product of the vector field (evaluated at the along the curve) and the derivative of the parameterization.
Here is the vector field evaluated along the curve (i.e. plug in \(x\) and \(y\) from the parameterization into the vector field).
\[\vec F\left( {\vec r\left( t \right)} \right) = {\left[ {{{\left( {t - 1} \right)}^2}} \right]^2}\,\vec i + \left( {{{\left( t \right)}^2} - 4} \right)\vec j = {\left( {t - 1} \right)^4}\,\vec i + \left( {{t^2} - 4} \right)\vec j\]The derivative of the parameterization is,
\[\vec r'\left( t \right) = \left\langle {1,2\left( {t - 1} \right)} \right\rangle \]Finally, the dot product of the vector field and the derivative of the parameterization.
\[\begin{align*}\vec F\left( {\vec r\left( t \right)} \right)\centerdot \vec r'\left( t \right) & = {\left( {t - 1} \right)^4}\left( 1 \right) + \left( {{t^2} - 4} \right)\left( {2t - 2} \right)\\ & = {\left( {t - 1} \right)^4} + 2{t^3} - 2{t^2} - 8t + 8\end{align*}\]Make sure that you simplify the dot product with an eye towards doing the integral!
Show Step 4Now all we need to do is evaluate the integral.
\[\begin{align*}\int\limits_{C}{{\vec F\centerdot d\vec r}} & = \int_{0}^{3}{{{{\left( {t - 1} \right)}^4} + 2{t^3} - 2{t^2} - 8t + 8\,dt}}\\ & = \left. {\left[ {\frac{1}{5}{{\left( {t - 1} \right)}^5} + \frac{1}{2}{t^4} - \frac{2}{3}{t^3} - 4{t^2} + 8t} \right]} \right|_0^3 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{171}}{{10}}}}\end{align*}\]