Section 16.4 : Line Integrals of Vector Fields
5. Evaluate \( \displaystyle \int\limits_{C}{{\vec F\centerdot d\vec r}}\) where \(\vec F\left( {x,y} \right) = 3y\,\vec i + \left( {{x^2} - y} \right)\vec j\) and \(C\) is the upper half of the circle centered at the origin of radius 1 with counter clockwise rotation and the portion of \(y = {x^2} - 1\) from \(x = - 1\) to \(x = 1\). See the sketch below.
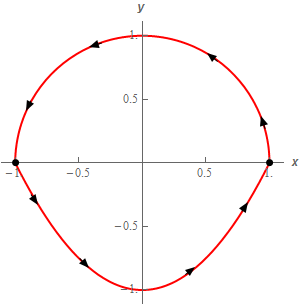
Show All Steps Hide All Steps
Start SolutionTo help with the problem let’s label each of the curves as follows,
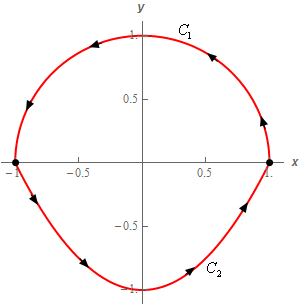
The parameterization of each curve is,
\({C_1}:\,\,\vec r\left( t \right) = \left\langle {\cos \left( t \right),\sin \left( t \right)} \right\rangle \hspace{0.25in}0 \le t \le \pi \)\({C_2}:\,\,\vec r\left( t \right) = \left\langle {t,{t^2} - 1} \right\rangle \hspace{0.25in} - 1 \le t \le 1\)
Show Step 2
Now we need to compute the line integral for each of the curves. In the first few problems in this section we evaluated the vector function along the curve, took the derivative of the parameterization and computed the dot product separately. For this problem we’ll be doing all that work in the integral itself.
Here is the line integral for each of the curves.
\[\begin{align*}\int\limits_{{{C_1}}}{{\vec F\centerdot d\vec r}} & = \int_{0}^{\pi }{{\left\langle {3\sin \left( t \right),{{\cos }^2}\left( t \right) - \sin \left( t \right)} \right\rangle \centerdot \left\langle { - \sin \left( t \right),\cos \left( t \right)} \right\rangle \,dt}}\\ & = \int_{0}^{\pi }{{ - 3{{\sin }^2}\left( t \right) + {{\cos }^3}\left( t \right) - \sin \left( t \right)\cos \left( t \right)\,dt}}\\ & = \int_{0}^{\pi }{{ - \frac{3}{2}\left( {1 - \cos \left( {2t} \right)} \right) + \cos \left( t \right)\left( {1 - {{\sin }^2}\left( t \right)} \right) - \frac{1}{2}\sin \left( {2t} \right)\,dt}}\\ & = \left. {\left( { - \frac{3}{2}\left( {t - \frac{1}{2}\sin \left( {2t} \right)} \right) + \sin \left( t \right) - \frac{1}{3}{{\sin }^3}\left( t \right) + \frac{1}{4}\cos \left( {2t} \right)\,dt} \right)} \right|_0^\pi = \underline { - \frac{3}{2}\pi } \end{align*}\] \[\begin{align*}\int\limits_{{{C_2}}}{{\vec F\centerdot d\vec r}} & = \int_{{ - 1}}^{1}{{\left\langle {3\left( {{t^2} - 1} \right),{t^2} - \left( {{t^2} - 1} \right)} \right\rangle \centerdot \left\langle {1,2t} \right\rangle \,dt}}\\ & = \int_{{ - 1}}^{1}{{3\left( {{t^2} - 1} \right) + 2t\,dt}}\\ & = \left. {\left( {{t^3} - 3t + {t^2}} \right)} \right|_{ - 1}^1 = \underline { - 4} \end{align*}\]You do recall how to deal with all those trig functions that we saw in the first integral don’t you? If not you should go back to the Calculus II material and work some practice problems. You’ll be seeing a fair number of integrals involving trig functions from this point on.
Show Step 3Okay to finish this problem out all we need to do is add up the line integrals over these curves to get the full line integral.
\[\int\limits_{C}{{\vec F\centerdot d\vec r}} = \left( { - \frac{3}{2}\pi } \right) + \left( { - 4} \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 4 - \frac{3}{2}\pi = - 8.7124}}\]Note that we put parenthesis around the result of each individual line integral simply to illustrate where it came from and they aren’t needed in general of course.