Section 17.5 : Stokes' Theorem
1. Use Stokes’ Theorem to evaluate \(\displaystyle \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}}\) where \(\vec F = y\,\vec i - x\,\vec j + y{x^3}\,\vec k\) and \(S\) is the portion of the sphere of radius 4 with \(z \ge 0\) and the upwards orientation.
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.
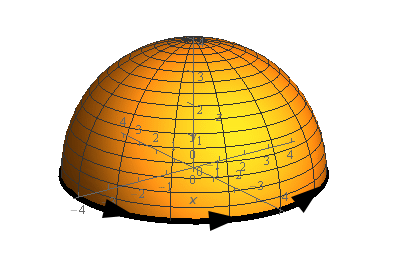
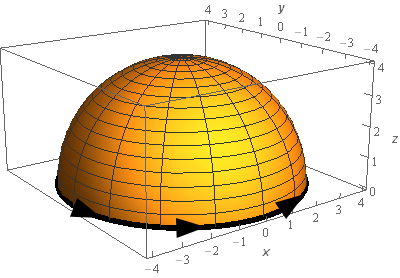
We included a sketch with traditional axes and a sketch with a set of “box” axes to help visualize the surface.
Because the orientation of the surface is upwards then all the normal vectors will be pointing outwards. So, if we walk along the edge of the surface, i.e. the curve \(C\), in the direction indicated with our head pointed away from the surface (i.e. in the same direction as the normal vectors) then our left hand will be over the region. Therefore the direction indicated in the sketch is the positive orientation of \(C\).
If you have trouble visualizing the direction of the curve simply get a cup or bowl and put it upside down on a piece of paper on a table. Sketch a set of axis on the piece of paper that will represent the plane the cup/bowl is sitting on to really help with the visualization. Then cut out a little stick figure and put a face on the “front” side of it and color the left hand a bright color so you can quickly see it. Now, on the edge of the cup/bowl/whatever you place the stick figure with it’s head pointing in the direction of the normal vectors (out away from the sphere/cup/bowl in our case) with its left hand over the surface. The direction that the “face” on the stick figure is facing is the direction you’d need to walk along the surface to get the positive orientation for \(C\).
Show Step 2We are going to use Stokes’ Theorem in the following direction.
\[\iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}} = \int\limits_{C}{{\vec F\centerdot d\vec r}}\]We’ve been given the vector field in the problem statement so we don’t need to worry about that. We will need to deal with \(C\).
Because \(C\) is just the curve along the bottom of the upper half of the sphere we can see that \(C\) in fact will be the intersection of the sphere and the \(xy\)-plane (i.e. \(z = 0\)). Therefore, \(C\) is just the circle of radius 4.
If we look at the sphere from above we get the following sketch of \(C\).
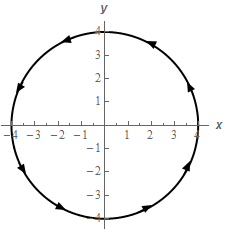
The parameterization of \(C\) is given by,
\[\vec r\left( t \right) = \left\langle {4\cos t,4\sin t,0} \right\rangle \hspace{0.25in}\hspace{0.25in}0 \le t \le 2\pi \]The \(z\) component of the parameterization is zero because \(C\) lies in the \(xy\)-plane.
Show Step 3Since we know we’ll need to eventually do the line integral we know we’ll need the following dot product.
\[\begin{align*}\vec F\left( {\vec r\left( t \right)} \right)\centerdot \vec r'\left( t \right) & = \left\langle {4\sin t, - 4\cos t,256\sin t{{\cos }^3}t} \right\rangle \centerdot \left\langle { - 4\sin t,4\cos t,0} \right\rangle \\ & = - 16{\sin ^2}t - 16{\cos ^2}t\\ & = - 16\end{align*}\]Don’t forget to plug the parameterization of \(C\) into the vector field!
Show Step 4Okay, let’s go ahead and evaluate the integral using Stokes’ Theorem.
\[\begin{align*}\iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}} & = \int\limits_{C}{{\vec F\centerdot d\vec r}}\\ & = \int_{0}^{{2\pi }}{{ - 16\,dt}} = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 32\pi }}\end{align*}\]