Section 17.5 : Stokes' Theorem

1. Use Stokes’ Theorem to evaluate \( \displaystyle \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}}\) where \(\vec F = y\,\vec i - x\,\vec j + y{x^3}\,\vec k\) and \(S\) is the portion of the sphere of radius 4 with \(z \ge 0\) and the upwards orientation. Solution
2. Use Stokes’ Theorem to evaluate \( \displaystyle \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}}\) where \(\vec F = \left( {{z^2} - 1} \right)\,\vec i + \left( {z + x{y^3}} \right)\,\vec j + 6\,\vec k\) and \(S\) is the portion of \(x = 6 - 4{y^2} - 4{z^2}\) in front of \(x = - 2\) with orientation in the negative \(x\)-axis direction. Solution
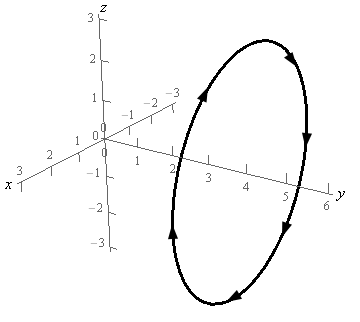
3. Use Stokes’ Theorem to evaluate \( \displaystyle \int\limits_{C}{{\vec F\centerdot d\vec r}}\) where \(\vec F = - yz\,\vec i + \left( {4y + 1} \right)\,\vec j + xy\,\vec k\) and \(C\) is is the circle of radius 3 at \(y = 4\) and perpendicular to the \(y\)-axis. \(C\) has a clockwise rotation if you are looking down the \(y\)-axis from the positive \(y\)-axis to the negative \(y\)-axis. See the figure below for a sketch of the curve.
   
   Solution
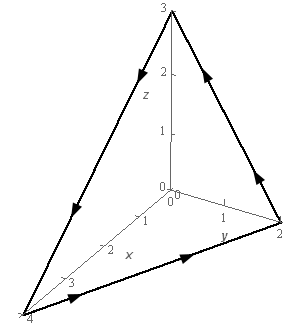
4. Use Stokes’ Theorem to evaluate \( \displaystyle \int\limits_{C}{{\vec F\centerdot d\vec r}}\) where \(\vec F = \left( {3y{x^2} + {z^3}} \right)\,\vec i + {y^2}\,\vec j + 4y{x^2}\,\vec k\) and \(C\) is is triangle with vertices \(\left( {0,0,3} \right)\), \(\left( {0,2,0} \right)\) and \(\left( {4,0,0} \right)\). \(C\) has a counter clockwise rotation if you are above the triangle and looking down towards the \(xy\)-plane. See the figure below for a sketch of the curve.
   
   Solution