Section 17.5 : Stokes' Theorem
3. Use Stokes’ Theorem to evaluate \(\displaystyle \int\limits_{C}{{\vec F\centerdot d\vec r}}\) where \(\vec F = - yz\,\vec i + \left( {4y + 1} \right)\,\vec j + xy\,\vec k\) and \(C\) is is the circle of radius 3 at \(y = 4\) and perpendicular to the \(y\)-axis. \(C\) has a clockwise rotation if you are looking down the \(y\)-axis from the positive \(y\)-axis to the negative \(y\)-axis. See the figure below for a sketch of the curve.
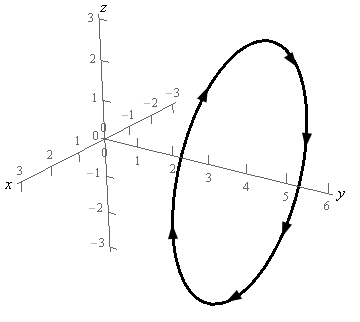
Show All Steps Hide All Steps
Start SolutionOkay, we are going to use Stokes’ Theorem in the following direction.
\[\int\limits_{C}{{\vec F\centerdot d\vec r}} = \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}}\]So, let’s first compute \({\mathop{\rm curl}\nolimits} \vec F\)since that is easy enough to compute and might be useful to have when we go to determine the surface \(S\) we’re going to integrate over.
The curl of the vector field is then,
\[{\mathop{\rm curl}\nolimits} \vec F = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\{\displaystyle \frac{\partial }{{\partial x}}}&{\displaystyle \frac{\partial }{{\partial y}}}&{\displaystyle \frac{\partial }{{\partial z}}}\\{ - yz}&{4y + 1}&{xy}\end{array}} \right| = x\vec i - y\vec j + z\vec k - y\vec j = \underline {x\vec i - 2y\vec j + z\vec k} \] Show Step 2Now we need to find a surface \(S\) with an orientation that will have a boundary curve that is the curve shown in the problem statement, including the correct orientation. This can seem to be a daunting task at times but it’s not as bad as it might appear to be. First we know that the boundary curve needs to be a circle. This means that we’re going to be looking for a surface whose cross section is a circle and we know of several surfaces that meet this requirement. We know that spheres, cones and elliptic paraboloids all have circles as cross sections.
The question becomes which of these surfaces would be best for us in this problem. To make this decision remember that we’ll eventually need to plug this surface into the vector field and then take the dot product of this with normal vector (which will also come from the surface of course).
In general, it won’t be immediately clear from the curl of the vector field by itself which surface we should use and that is the case here. The curl of the vector field has all three components and none of them are that difficult to deal with but there isn’t anything that suggests one surface might be easier than the other.
So, let’s consider a sphere first. The issue with spheres is that its parameterization and normal vector are lengthy and many lead to messy integrands. So, because the curl of the vector field does have all three components to it which may well lead to long and/or messy integrands we’ll not work with a sphere for this problem.
Now let’s think about a cone. Equations of cones aren’t that bad but they will involve a square root and in this case would need to be in the form \(y = \sqrt {a{x^2} + b{z^2}} \) because the boundary curve is centered on the \(y\)-axis. The normal vector will also contain roots and this will often lead to messy integrands. So, let’s not work with a cone either in this problem.
That leaves elliptic paraboloids and we probably should have considered them first. The equations are simple and the normal vectors are even simpler so they seem like a good choice of surface for this problem.
Note that we’re not saying that spheres and cones are never good choices for the surface. For some vector fields the curl may end up being very simple with one of these surfaces and so they would be perfectly good choices.
Show Step 3We have two possibilities for elliptic paraboloids that we could use here. Both will be centered on the \(y\)-axis but one will open in the negative \(y\) direction while the other will open in the positive \(y\) direction.
Here is a couple of sketches of possible elliptic paraboloids we could use here.
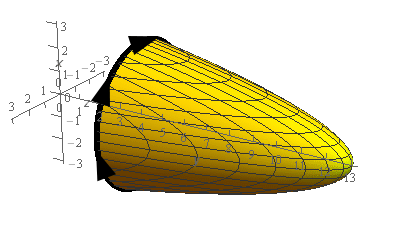

Let’s get an equation for each of these. Note that for each of these if we set the equation of the paraboloid and the plane \(y = 4\) equal we need to get the circle \({x^2} + {z^2} = 9\) since this is the boundary curve that should occur at \(y = 4\).
Let’s get the equation of the first paraboloid (the one that opens in the negative \(y\) direction. We know that the equation of this paraboloid should be \(y = a - {x^2} - {z^2}\) for some value of \(a\). As noted if we set this equal to \(y = 4\) and do some simplification we know what equation we should get. So, let’s set the two equations equal.
\[4 = a - {x^2} - {z^2}\hspace{0.25in} \to \hspace{0.25in}\,{x^2} + {z^2} = a - 4 = 9\hspace{0.25in} \to \hspace{0.25in}a = 13\]As shown we know that the \(a - 4\) should be 9 and so we must have \(a = 13\). Therefore, the equation of the paraboloid that open in the negative \(y\) direction is,
\[y = 13 - {x^2} - {z^2}\]Next, let’s get the equation of the paraboloid that opens in the positive \(y\) direction. The equation of this paraboloid will be in the form \(y = {x^2} + {z^2} + a\) for some \(a\). Setting this equal to \(y = 4\) gives,
\[4 = {x^2} + {z^2} + a\hspace{0.25in} \to \hspace{0.25in}\,{x^2} + {z^2} = 4 - a = 9\hspace{0.25in} \to \hspace{0.25in}a = - 5\]The equation of the paraboloid that opens in the positive \(y\) direction is then,
\[y = {x^2} + {z^2} - 5\]Either of these surfaces could be used to do this problem.
Show Step 4We now need to determine the orientation of the normal vectors that will induce a positive orientation of the boundary curve, \(C\), that matches the orientation that was given in the problem statement.
We’ll find the normal vectors for each surface despite the fact that we really only need to do it for one of them since we only need one of the surfaces to do the problem as noted in the previous step. Determining the orientation of the surface can be a little tricky for some folks so doing an extra one might help see what’s going on here.
Remember that what we want to do here is think of ourselves as walking along the boundary curve of the surface in the direction indicated while our left hand is over the surface itself. We now need to determine if we are walking along the outside of the surface or the inside of the surface.
If we are walking along the outside of the surface then our heads, and hence the normal vectors, will be pointing away from the region enclosed by the surface. On the other hand, if we are walking along the inside of the surface then our heads, and hence the normal vectors, will be pointing into the region enclosed by the surface.
To help visualize this for our two surfaces it might help to get a cup or bowl that we can use to represent the surface. The edge of the cup/bowl will then represent the boundary curve. Next cut out a stick figure and put a face on one side so we know which direction we’ll be walking and brightly color the left hand to make it really clear which side is the left side.
Now, put the cup/bowl on its side so it looks vaguely like the surface we’re working with and put the stick figure on the edge with the face pointing in the direction the curve is moving and the left hand over the cup/bowl. Do we need to put the stick figure on the inside or outside of the cup/bowl to do this?
Okay, let’s do this for the first surface, \(y = 13 - {x^2} - {z^2}\). In this case our stick figure would need to be standing on the inside of the cup/bowl/surface. Therefore, the normal vectors on the surface would all need to be point in towards the region enclosed by the surface. This also will mean that all the normal vectors will need to have a negative \(y\) component. Again, to visualize this take the stick figure and move it into the region and toward the end of cup/bowl/surface and you’ll see it start to point more and more in the negative \(y\) direction (and hence will have a negative \(y\) component). Note that the \(x\) and \(z\) component can be either positive or negative depending on just where we are on the interior of the surface.
Now, let’s take a look at the first surface, \(y = {x^2} + {z^2} - 5\). For this surface our stick figure would need to be standing on the outside of the cup/bowl/surface. So, in this case, the normal vectors would point out away from the region enclosed by the surface. These will also have a negative \(y\) component and you can use the method we discussed in the above paragraph to help visualize this.
Show Step 5We now need to start thinking about actually computing the integral. We’ll write the equation of the surface as,
\[f\left( {x,y,z} \right) = 13 - {x^2} - {z^2} - y = 0\]A unit normal vector for the surface is then,
\[\vec n = \frac{{\nabla f}}{{\left\| {\nabla f} \right\|}} = \frac{{\left\langle { - 2x, - 1, - 2z} \right\rangle }}{{\left\| {\nabla f} \right\|}}\]We didn’t compute the magnitude of the gradient since we know that it will just cancel out when we start working with the integral.
Note as well that this does have the correct orientation because the \(y\) component is negative.
Next, we’ll need to compute the following dot product.
\[\begin{align*}{\mathop{\rm curl}\nolimits} \vec F\centerdot \vec n & = \left\langle {x, - 2\left( {13 - {x^2} - {z^2}} \right),z} \right\rangle \centerdot \frac{{\left\langle { - 2x, - 1, - 2z} \right\rangle }}{{\left\| {\nabla f} \right\|}}\\ & = \frac{1}{{\left\| {\nabla f} \right\|}}\left( { - 2{x^2} + 2\left( {13 - {x^2} - {z^2}} \right) - 2{z^2}} \right)\\ & = \frac{1}{{\left\| {\nabla f} \right\|}}\left( {26 - 4{x^2} - 4{z^2}} \right)\end{align*}\] Show Step 6Now, applying Stokes’ Theorem to the integral and converting to a “normal” double integral gives,
\[\begin{align*}\int\limits_{C}{{\vec F\centerdot d\vec r}} & = \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}}\\ & = \iint\limits_{S}{{\frac{1}{{\left\| {\nabla f} \right\|}}\left( {26 - 4{x^2} - 4{z^2}} \right)dS}}\\ & = \iint\limits_{D}{{\frac{1}{{\left\| {\nabla f} \right\|}}\left( {26 - 4{x^2} - 4{z^2}} \right)\left\| {\nabla f} \right\|dA}}\\ & = \iint\limits_{D}{{26 - 4{x^2} - 4{z^2}dA}}\end{align*}\] Show Step 7To finish this integral out then we’ll need to convert to polar coordinates using the following polar coordinates.
\[x = r\cos \theta \hspace{0.25in}\hspace{0.25in}z = r\sin \theta \hspace{0.25in}\hspace{0.25in}{x^2} + {z^2} = {r^2}\]In this case \(D\) is just the disk \({x^2} + {z^2} \le 9\) and so the limits for the integral are,
\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le 3\end{array}\]The integral is then,
\[\begin{align*}\int\limits_{C}{{\vec F\centerdot d\vec r}}& = \iint\limits_{S}{{{\mathop{\rm curl}\nolimits} \vec F\centerdot d\vec S}}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{3}{{\left( {26 - 4{r^2}} \right)r\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{3}{{26r - 4{r^3}\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\left. {\left( {13{r^2} - {r^4}} \right)} \right|_0^3\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{36\,d\theta }}\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{72\pi }}\end{align*}\]Don’t forget to pick up an extra \(r\) from converting the \(dA\) to polar coordinates.