Section 17.4 : Surface Integrals of Vector Fields
2. Evaluate \( \displaystyle \iint\limits_{S}{{\vec F\centerdot \,d\vec S}}\) where \(\vec F = - x\,\vec i + 2y\,\vec j - z\,\vec k\) and \(S\) is the portion of \(y = 3{x^2} + 3{z^2}\) that lies behind \(y = 6\) oriented in the positive \(y\)-axis direction.
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.
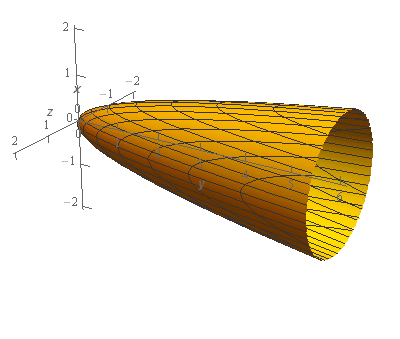
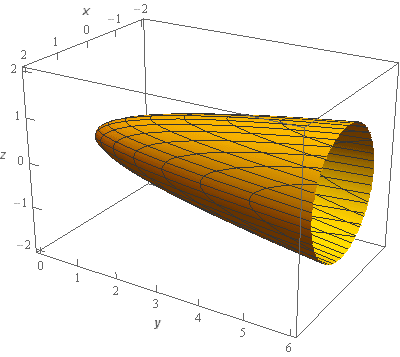
Note that the surface in this problem is only the elliptic paraboloid and does not include the “cap” at \(y = 6\). We would only include the “cap” if the problem had specified that in some manner to make it clear.
In this case \(D\) will be the circle/disk we get by setting the two equations equal or,
\[6 = 3{x^2} + 3{z^2}\hspace{0.25in} \Rightarrow \hspace{0.25in}{x^2} + {z^2} = 2\]So, \(D\) will be the disk \({x^2} + {z^2} \le 2\).
Show Step 2Let’s get the integral set up now. In this case the we can write the equation of the surface as follows,
\[f\left( {x,y,z} \right) = 3{x^2} + 3{z^2} - y = 0\]A unit normal vector for the surface is then,
\[\vec n = \frac{{\nabla f}}{{\left\| {\nabla f} \right\|}} = \frac{{\left\langle {6x, - 1,6z} \right\rangle }}{{\left\| {\nabla f} \right\|}}\]We didn’t compute the magnitude of the gradient since we know that it will just cancel out when we start working with the integral.
Note as well that, in this case, the normal vector we computed above does not have the correct orientation. We were told in the problem statement that the orientation was in the positive \(y\)-axis direction and this means that the normal vector should always point in the general direction of the positive \(y\)-axis (i.e. a positive \(y\) component) and this one does not.
That is easy to fix however. All we need to do is multiply the above normal vector by minus one and we’ll get what we need. So, here is the normal vector we need for this problem.
\[\vec n = - \frac{{\nabla f}}{{\left\| {\nabla f} \right\|}} = \frac{{\left\langle { - 6x,1, - 6z} \right\rangle }}{{\left\| {\nabla f} \right\|}}\]As we can see this normal vector does in fact have a positive \(y\) component as we need.
Show Step 3Next, we’ll need to compute the following dot product.
\[\begin{align*}\vec F\left( {x,3{x^2} + 3{z^2},z} \right)\centerdot \vec n & = \left\langle { - x,2\left( {3{x^2} + 3{z^2}} \right), - z} \right\rangle \centerdot \frac{{\left\langle { - 6x,1, - 6z} \right\rangle }}{{\left\| {\nabla f} \right\|}}\\ & = \frac{1}{{\left\| {\nabla f} \right\|}}\left( {6{x^2} + 2\left( {3{x^2} + 3{z^2}} \right) + 6{z^2}} \right)\\ & = \frac{1}{{\left\| {\nabla f} \right\|}}\left[ {12\left( {{x^2} + {z^2}} \right)} \right]\end{align*}\]Remember that we needed to plug in the equation of the surface, \(y = 3{x^2} + 3{z^2}\), into \(y\) in the vector field!
The integral is then,
\[\begin{align*}\iint\limits_{S}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{S}{{\frac{1}{{\left\| {\nabla f} \right\|}}\left[ {12\left( {{x^2} + {z^2}} \right)} \right]\,dS}}\\ & = \iint\limits_{D}{{\frac{1}{{\left\| {\nabla f} \right\|}}\left[ {12\left( {{x^2} + {z^2}} \right)} \right]\left\| {\nabla f} \right\|\,dA}}\\ & = \iint\limits_{D}{{12\left( {{x^2} + {z^2}} \right)\,dA}}\end{align*}\]As noted above we didn’t need to compute the magnitude of the gradient since it would just cancel out when we converted the surface integral into a “normal” double integral.
Also, recall that \(D\) was given in Step 1 and is just the disk \({x^2} + {z^2} \le 2\)
Show Step 4Now all that we need to do is evaluate the double integral and that shouldn’t be too difficult at this point.
Note as well that we’ll want to use polar coordinates in the double integral. We’ll use the following set of polar coordinates.
\[x = r\cos \theta \hspace{0.25in}\hspace{0.25in}z = r\sin \theta \hspace{0.25in}\hspace{0.25in}{x^2} + {z^2} = {r^2}\]The polar limits for \(D\) are,
\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le \sqrt 2 \end{array}\]The integral is then,
\[\begin{align*}\iint\limits_{S}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{D}{{12\left( {{x^2} + {z^2}} \right)\,dA}}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{{\sqrt 2 }}{{12{r^3}\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\left. {3{r^4}} \right|_0^{\sqrt 2 }\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{12\,d\theta }} = \require{bbox} \bbox[2pt,border:1px solid black]{{24\pi }}\end{align*}\]Don’t forget that we pick up an extra \(r\) from the \(dA\) when converting to polar coordinates.