Section 17.3 : Surface Integrals
3. Evaluate \( \displaystyle \iint\limits_{S}{{2y\,dS}}\) where \(S\) is the portion of \({y^2} + {z^2} = 4\) between \(x = 0\) and \(x = 3 - z\).
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.

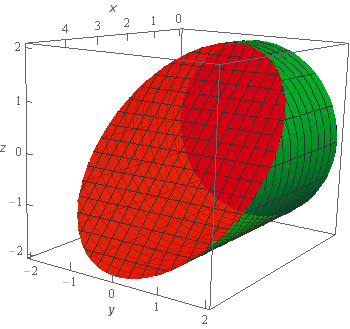
Note that the surface in this problem is only the cylinder itself. The “caps” of the cylinder are not part of this surface despite the red “cap” in the sketch. That was included in the sketch to make the front edge of the cylinder clear in the sketch. We would only include the “caps” if the problem had specified that in some manner to make it clear.
Show Step 2Now because our surface is a cylinder we’ll need to parameterize it and use the following formula for the surface integral.
\[\iint\limits_{S}{{f\left( {x,y,z} \right)\,dS}} = \iint\limits_{D}{{f\left( {\vec r\left( {u,v} \right)} \right)\left\| {{{\vec r}_u} \times {{\vec r}_v}} \right\|\,dA}}\]where \(u\) and \(v\) will be chosen as needed when doing the parameterization.
We saw how to parameterize a cylinder in the previous section so we won’t go into detail for the parameterization. The parameterization is,
\[\vec r\left( {x,\theta } \right) = \left\langle {x,2\sin \theta ,2\cos \theta } \right\rangle \hspace{0.25in}\,\,\,\,\,0 \le \theta \le 2\pi ,\,\,\,\,\,0 \le x \le 3 - z = 3 - 2\cos \theta \]We’ll use the full range of \(\theta \) since we are allowing it to rotate all the way around the x‑axis. The \(x\) limits come from the two planes that “bound” the cylinder and we’ll need to convert the upper limit using the parameterization.
Next, we’ll need to compute the cross product.
\[{\vec r_x} = \left\langle {1,0,0} \right\rangle \hspace{0.25in}{\vec r_\theta } = \left\langle {0,2\cos \theta , - 2\sin \theta } \right\rangle \] \[{\vec r_x} \times {\vec r_\theta } = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\1&0&0\\0&{2\cos \theta }&{ - 2\sin \theta }\end{array}} \right| = 2\sin \theta \vec j + 2\cos \theta \vec k\]The magnitude of the cross product is,
\[\left\| {{{\vec r}_x} \times {{\vec r}_\theta }} \right\| = \sqrt {4{{\sin }^2}\theta + 4{{\cos }^2}\theta } = 2\]The integral is then,
\[\iint\limits_{S}{{2y\,dS}} = \iint\limits_{D}{{2\left( {2\sin \theta } \right)\left( 2 \right)\,dA}} = \iint\limits_{D}{{8\sin \theta \,dA}}\]Don’t forget to plug the \(y\) component of the surface parametrization into the integrand and \(D\) is just the limits on \(x\) and \(\theta \) we noted above in the parameterization.
Show Step 3Now all that we need to do is evaluate the double integral and that shouldn’t be too difficult at this point.
The integral is then,
\[\begin{align*}\iint\limits_{S}{{2y\,dS}} & = \int_{0}^{{2\pi }}{{\int_{0}^{{3 - 2\cos \theta }}{{8\sin \theta \,dx}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\left. {\left( {8x\sin \theta } \right)} \right|_0^{3 - 2\cos \theta }\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{8\left( {3 - 2\cos \theta } \right)\sin \theta \,d\theta }}\\ & = \int_{0}^{{2\pi }}{{24\sin \theta - 16\sin \theta \cos \theta \,d\theta }}\\ & = \int_{0}^{{2\pi }}{{24\sin \theta - 8\sin \left( {2\theta } \right)\,d\theta }}\\ & = \left. {\left( { - 24\cos \theta + 4\cos \left( {2\theta } \right)\,} \right)} \right|_0^{2\pi } = \require{bbox} \bbox[2pt,border:1px solid black]{0}\end{align*}\]