Section 17.3 : Surface Integrals
4. Evaluate \( \displaystyle \iint\limits_{S}{{xz\,dS}}\) where \(S\) is the portion of the sphere of radius 3 with \(x \le 0\), \(y \ge 0\) and \(z \ge 0\).
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.
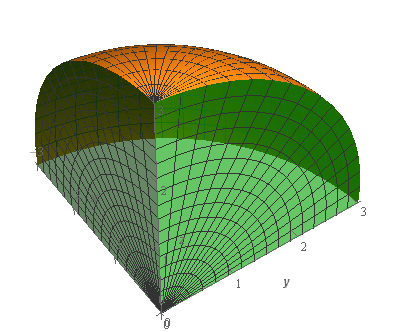
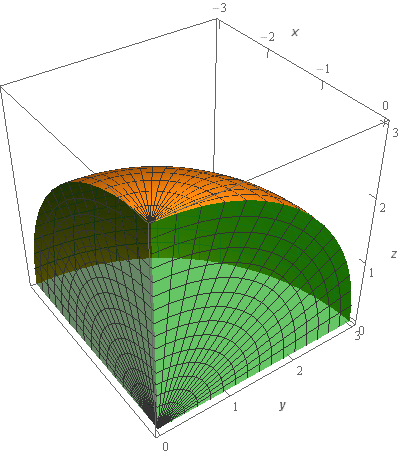
Note that the surface in this problem is only the part of the sphere itself. The “edges” (the greenish portions on the right/left) are not part of this surface despite the fact that they are in the sketch. They were included in the sketch to try and make the surface a little clearer in the sketch. We would only include the “edges” if the problem had specified that in some manner to make it clear.
Show Step 2Now because our surface is a sphere we’ll need to parameterize it and use the following formula for the surface integral.
\[\iint\limits_{S}{{f\left( {x,y,z} \right)\,dS}} = \iint\limits_{D}{{f\left( {\vec r\left( {u,v} \right)} \right)\left\| {{{\vec r}_u} \times {{\vec r}_v}} \right\|\,dA}}\]where \(u\) and \(v\) will be chosen as needed when doing the parameterization.
We saw how to parameterize a sphere in the previous section so we won’t go into detail for the parameterization. The parameterization is,
\[\vec r\left( {\theta ,\varphi } \right) = \left\langle {3\sin \varphi \cos \theta ,3\sin \varphi \sin \theta ,3\cos \varphi } \right\rangle \hspace{0.25in}\,\,\,\,\,\frac{1}{2}\pi \le \theta \le \pi ,\,\,\,\,\,0 \le \varphi \le \frac{1}{2}\pi \]We needed the restriction on \(\varphi \) to make sure that we only get a portion of the upper half of the sphere (i.e.\(z \ge 0\)). Likewise the restriction on \(\theta \) was needed to get only the portion that was in the 2nd quadrant of the \(xy\)-plane (i.e. \(x \le 0\) and \(y \ge 0\)).
Next, we’ll need to compute the cross product.
\[{\vec r_\theta } = \left\langle { - 3\sin \varphi \sin \theta ,3\sin \varphi \cos \theta ,0} \right\rangle \hspace{0.25in}\hspace{0.25in}{\vec r_\varphi } = \left\langle {3\cos \varphi \cos \theta ,3\cos \varphi \sin \theta , - 3\sin \varphi } \right\rangle \] \[\begin{align*}{{\vec r}_\theta } \times {{\vec r}_\varphi } & = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\{ - 3\sin \varphi \sin \theta }&{3\sin \varphi \cos \theta }&0\\{3\cos \varphi \cos \theta }&{3\cos \varphi \sin \theta }&{ - 3\sin \varphi }\end{array}} \right|\\ & = - 9{\sin ^2}\varphi \cos \theta \,\vec i - 9\sin \varphi \cos \varphi {\sin ^2}\theta \vec k - 9\sin \varphi \cos \varphi {\cos ^2}\theta \vec k - 9{\sin ^2}\varphi \sin \theta \vec j\\ & = - 9{\sin ^2}\varphi \cos \theta \,\vec i - 9{\sin ^2}\varphi \sin \theta \vec j - 9\sin \varphi \cos \varphi \left( {{{\sin }^2}\theta + {{\cos }^2}\theta } \right)\vec k\\ & = - 9{\sin ^2}\varphi \cos \theta \,\vec i - 9{\sin ^2}\varphi \sin \theta \vec j - 9\sin \varphi \cos \varphi \vec k\end{align*}\]The magnitude of the cross product is,
\[\begin{align*}\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\| & = \sqrt {{{\left( { - 9{{\sin }^2}\varphi \cos \theta } \right)}^2} + {{\left( { - 9{{\sin }^2}\varphi \sin \theta } \right)}^2} + {{\left( { - 9\sin \varphi \cos \varphi } \right)}^2}} \\ & = \sqrt {81{{\sin }^4}\varphi \left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right) + 81{{\sin }^2}\varphi {{\cos }^2}\varphi } \\ & = \sqrt {81{{\sin }^2}\varphi \left( {{{\sin }^2}\varphi + {{\cos }^2}\varphi } \right)} \\ & = 9\left| {\sin \varphi } \right|\\ & = 9\sin \varphi \end{align*}\]The integral is then,
\[\iint\limits_{S}{{xz\,dS}} = \iint\limits_{D}{{\left( {3\sin \varphi \cos \theta } \right)\left( {3\cos \varphi } \right)\left( {9\sin \varphi } \right)\,dA}} = \iint\limits_{D}{{81\cos \varphi {{\sin }^2}\varphi \cos \theta \,dA}}\]Don’t forget to plug the \(x\) and \(z\) component of the surface parameterization into the integrand and \(D\) is just the limits on \(\theta \) and \(\varphi \) we noted above in the parameterization.
Show Step 3Now all that we need to do is evaluate the double integral and that shouldn’t be too difficult at this point.
The integral is then,
\[\begin{align*}\iint\limits_{S}{{xz\,dS}} & = \iint\limits_{D}{{81\cos \varphi {{\sin }^2}\varphi \cos \theta \,dA}}\\ & = \int_{{\frac{1}{2}\pi }}^{\pi }{{\int_{0}^{{\frac{1}{2}\pi }}{{81\cos \varphi {{\sin }^2}\varphi \cos \theta \,d\varphi }}\,d\theta }}\\ & = \int_{{\frac{1}{2}\pi }}^{\pi }{{\left. {\left( {27{{\sin }^3}\varphi \cos \theta \,d\varphi } \right)} \right|_0^{\frac{1}{2}\pi }\,d\theta }}\\ & = \int_{{\frac{1}{2}\pi }}^{\pi }{{27\cos \theta \,d\theta }}\\ & = \left. {\left( {27\sin \theta } \right)} \right|_{\frac{1}{2}\pi }^\pi = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 27}}\end{align*}\]