Section 17.3 : Surface Integrals
5. Evaluate \( \displaystyle \iint\limits_{S}{{yz + 4xy\,dS}}\) where \(S\) is the surface of the solid bounded by \(4x + 2y + z = 8\), \(z = 0\), \(y = 0\) and \(x = 0\). Note that all four surfaces of this solid are included in \(S\).
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.
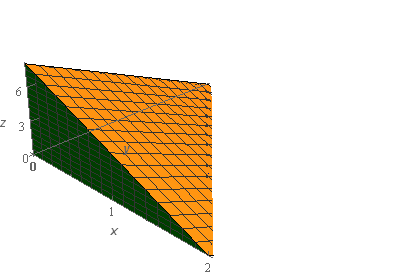
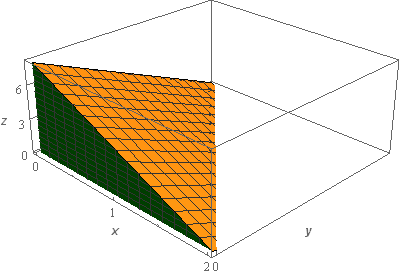
Okay, as noted in the problem statement all four surfaces in the sketch (two not shown) are part of \(S\) so let’s define each of them as follows.
\({S_1}:{\mbox{ Plane given by }}4x + 2y + z = 8{\mbox{ }}\left( {i.e{\mbox{ the top of the solid}}} \right)\)
\({S_2}:{\mbox{ Plane given by }}y = 0{\mbox{ }}\left( {i.e{\mbox{ the triangle on right side of the solid}}} \right)\)
\({S_3}:{\mbox{ Plane given by }}x = 0{\mbox{ }}\left( {i.e{\mbox{ the triangle at back of the solid - not shown in sketch}}} \right)\)
\({S_4}:{\mbox{ Plane given by }}z = 0{\mbox{ }}\left( {i.e{\mbox{ the triangle on bottom of the solid - not shown in sketch}}} \right)\)
As noted in the definitions above the first two surfaces are shown in the sketch but the last two are not actually shown due to the orientation of the solid. Below are sketches of each of the three surfaces that correspond to the coordinates planes.
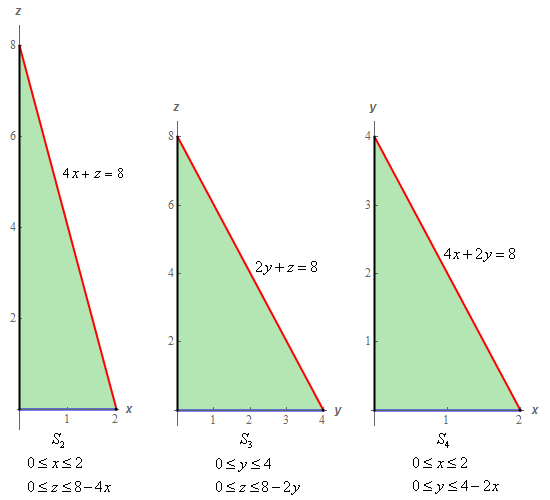
With each of the sketches we gave limits on the variables for each of them since we’ll eventually need that when we start doing the surface integral along each surface.
Now we need to go through and do the integral for each of these surfaces and we’re going to go through these a little quicker than we did for the first few problems in this section.
Show Step 2Let’s start with \({S_1}\). In this case the surface can easily be solved for \(z\) to get,
\[z = 8 - 4x - 2y\]With the equation of the surface written in this manner the region \(D\) will be in the xy‑plane and if you think about it you’ll see that in fact \(D\) is nothing more than \({S_4}\)!
The integral in this case is,
\[\begin{align*}\iint\limits_{{{S_1}}}{{yz + 4xy\,dS}} & = \iint\limits_{D}{{\left[ {y\left( {8 - 4x - 2y} \right) + 4xy} \right]\sqrt {{{\left( { - 4} \right)}^2} + {{\left( { - 2} \right)}^2} + 1} \,dA}}\\ & = \sqrt {21} \iint\limits_{D}{{8y - 2{y^2}\,dA}}\end{align*}\]Don’t forget to plug the equation of the surface into \(z\) in the integrand and don’t forget to use the equation of the surface in the computation of the root!
Now, as noted above \(D\) for this surface is nothing more than \({S_4}\) and so we can use the limits from the sketch of \({S_4}\) in Step 1.
Now let’s compute the integral for this surface.
\[\begin{align*}\iint\limits_{{{S_1}}}{{yz + 4xy\,dS}} & = \sqrt {21} \int_{0}^{2}{{\int_{0}^{{4 - 2x}}{{8y - 2{y^2}\,dy}}\,dx}}\\ & = \sqrt {21} \int_{0}^{2}{{\left. {\left[ {4{y^2} - \frac{2}{3}{y^3}} \right]} \right|_0^{4 - 2x}\,dx}}\\ & = \sqrt {21} \int_{0}^{2}{{4{{\left( {4 - 2x} \right)}^2} - \frac{2}{3}{{\left( {4 - 2x} \right)}^3}\,dx}}\\ & = \sqrt {21} \left. {\left[ { - \frac{2}{3}{{\left( {4 - 2x} \right)}^3} + \frac{1}{{12}}{{\left( {4 - 2x} \right)}^4}} \right]} \right|_0^2 = \underline {\frac{{64\sqrt {21} }}{3} = 97.7616} \end{align*}\] Show Step 3Next we’ll take care of \({S_2}\). In this case the equation for the surface is simply \(y = 0\) and \(D\) is given in the sketch of \({S_2}\) in Step 1.
The integral in this case is,
\[\iint\limits_{{{S_2}}}{{yz + 4xy\,dS}} = \iint\limits_{D}{{0\sqrt {{{\left( 0 \right)}^2} + 1 + {{\left( 0 \right)}^2}} \,dA}} = \iint\limits_{D}{{0\,dA}} = \underline 0 \]So, in this case we didn’t need to actually compute the integral. Sometimes we’ll get lucky like this, although it probably won’t happen all that often.
Show Step 4Now we can take care of \({S_3}\). In this case the equation for the surface is simply \(x = 0\) and \(D\) is given in the sketch of \({S_3}\) in Step 1.
The integral in this case is,
\[\iint\limits_{{{S_3}}}{{yz + 4xy\,dS}} = \iint\limits_{D}{{\left[ {yz + 4\left( 0 \right)y} \right]\sqrt {1 + {{\left( 0 \right)}^2} + {{\left( 0 \right)}^2}} \,dA}} = \iint\limits_{D}{{yz\,dA}}\]Don’t forget to plug the equation of the surface into \(x\) in the integrand and don’t forget to use the equation of the surface in the computation of the root (although in this case the root just evaluates to one)!
Using the limits for \(D\) from the sketch in Step 1 we can quickly evaluate the integral for this surface.
\[\begin{align*}\iint\limits_{{{S_3}}}{{yz + 4xy\,dS}} & = \int_{0}^{4}{{\int_{0}^{{8 - 2y}}{{yz\,dz}}\,dy}}\\ & = \int_{0}^{4}{{\left. {\left[ {\frac{1}{2}y{z^2}} \right]} \right|_0^{8 - 2y}\,dy}}\\ & = \int_{0}^{4}{{32y - 16{y^2} + 2{y^3}\,dy}}\\ & = \left. {\left[ {16{y^2} - \frac{{16}}{3}{y^3} + \frac{1}{2}{y^4}} \right]} \right|_0^4 = \underline {\frac{{128}}{3} = 42.6667} \end{align*}\] Show Step 5Finally let’s take care of \({S_4}\). In this case the equation for the surface is simply \(z = 0\) and \(D\) is given in the sketch of \({S_4}\) in Step 1.
The integral in this case is,
\[\iint\limits_{{{S_4}}}{{yz + 4xy\,dS}} = \iint\limits_{D}{{\left[ {y\left( 0 \right) + 4xy} \right]\sqrt {{{\left( 0 \right)}^2} + {{\left( 0 \right)}^2} + 1} \,dA}} = \iint\limits_{D}{{4xy\,dA}}\]Don’t forget to plug the equation of the surface into \(z\) in the integrand and don’t forget to use the equation of the surface in the computation of the root (although in this case the root just evaluates to one)!
Using the limits for \(D\) from the sketch in Step 1 we can quickly evaluate the integral for this surface.
\[\begin{align*}\iint\limits_{{{S_4}}}{{yz + 4xy\,dS}} & = \int_{0}^{2}{{\int_{0}^{{4 - 2x}}{{4xy\,dy}}\,dx}}\\ & = \int_{0}^{2}{{\left. {\left[ {2x{y^2}} \right]} \right|_0^{4 - 2x}\,dx}}\\ & = \int_{0}^{2}{{32x - 32{x^2} + 8{x^3}\,dx}}\\ & = \left. {\left[ {16{x^2} - \frac{{32}}{3}{x^3} + 2{x^4}} \right]} \right|_0^2 = \underline {\frac{{32}}{3} = 10.6667} \end{align*}\] Show Step 6Now, to get the value of the integral over the full surface all we need to do is sum up the values of each of the integrals over the four surfaces above. Doing this gives,
\[\iint\limits_{S}{{yz + 4xy\,dS}} = \left( {\frac{{64\sqrt {21} }}{3}} \right) + \left( 0 \right) + \left( {\frac{{128}}{3}} \right) + \left( {\frac{{32}}{3}} \right) = \frac{{64\sqrt {21} }}{3} + \frac{{160}}{3} = \require{bbox} \bbox[2pt,border:1px solid black]{{151.0949}}\]We put parenthesis around each of the individual integral values just to indicate where each came from. In general, these aren’t needed of course.