Section 15.7 : Triple Integrals in Spherical Coordinates
2. Evaluate \( \displaystyle \iiint\limits_{E}{{{x^2} + {y^2}\,dV}}\) where \(E\) is the region portion of \({x^2} + {y^2} + {z^2} = 4\) with \(y \ge 0\).
Show All Steps Hide All Steps
Start SolutionOkay, let’s start off with a quick sketch of the region \(E\) so we can get a feel for what we’re dealing with.

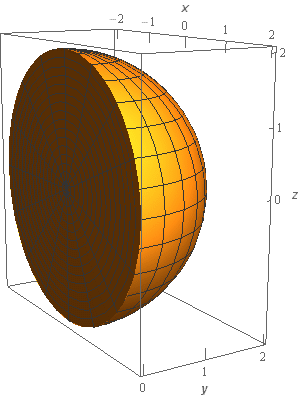
We’ve given the sketches with a set of “traditional” axes as well as a set of “box” axes to help visualize the surface and region.
In this case we’re dealing with the portion of the sphere of radius 2 with \(y \ge 0\) .
Show Step 2Now, since we are integrating over a portion of a sphere it makes sense to use spherical coordinate for the integral and the limits are,
\[\begin{array}{c}0 \le \varphi \le \pi \\ 0 \le \theta \le \pi \\ 0 \le \rho \le 2\end{array}\]Remember that \(\varphi \) is the angle from the positive \(z\)-axis that we rotate through as we cover the region and \(\theta \) is the angle we rotate around the \(z\)-axis as we cover the region.
In this case we have only the portion of the sphere with \(y \ge 0\) and so \(\theta \) will range from 0 to \(\pi \) (remember that we measure \(\theta \) from the positive \(x\)-axis). Because we want the full half of the sphere with \(y \ge 0\) we know that \(\varphi \) will range from 0 to \(\pi \).
Show Step 3Plugging these limits into the integral and converting to spherical coordinates gives,
\[\begin{align*}\iiint\limits_{E}{{{x^2} + {y^2}\,dV}} & = \int_{0}^{\pi }{{\int_{0}^{\pi }{{\int_{0}^{2}{{\left[ {{{\left( {\rho \sin \varphi \cos \theta } \right)}^2} + {{\left( {\rho \sin \varphi \sin \theta } \right)}^2}} \right]\left( {{\rho ^2}\sin \varphi } \right)\,d\rho }}\,d\theta }}\,d\varphi }}\\ & = \int_{0}^{\pi }{{\int_{0}^{\pi }{{\int_{0}^{2}{{\left[ {{\rho ^2}{{\sin }^2}\varphi {{\cos }^2}\theta + {\rho ^2}{{\sin }^2}\varphi {{\sin }^2}\theta } \right]\left( {{\rho ^2}\sin \varphi } \right)\,d\rho }}\,d\theta }}\,d\varphi }}\\ & = \int_{0}^{\pi }{{\int_{0}^{\pi }{{\int_{0}^{2}{{\left[ {{\rho ^2}{{\sin }^2}\varphi \left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right)} \right]\left( {{\rho ^2}\sin \varphi } \right)\,d\rho }}\,d\theta }}\,d\varphi }}\\ & = \int_{0}^{\pi }{{\int_{0}^{\pi }{{\int_{0}^{2}{{{\rho ^4}{{\sin }^3}\varphi \,d\rho }}\,d\theta }}\,d\varphi }}\end{align*}\]Don’t forget to convert the \(x\) and \(y\) into spherical coordinates and also don’t forget that \(dV = {\rho ^2}\sin \varphi \,d\rho \,d\theta \,d\varphi \) and so we’ll pick up a couple of extra terms when converting the \(dV\) to spherical coordinates.
In this case we also did a fair amount of simplification that will definitely make the integration easier to deal with. Don’t forget to do this kind of simplification when possible!
Show Step 4Okay, now all we need to do is evaluate the integral. Here is the \(\rho \) integration.
\[\begin{align*}\iiint\limits_{E}{{{x^2} + {y^2}\,dV}} & = \int_{0}^{\pi }{{\int_{0}^{\pi }{{\left. {\left( {\frac{1}{5}{\rho ^5}{{\sin }^3}\varphi } \right)} \right|_0^2\,d\theta }}\,d\varphi }}\\ & = \int_{0}^{\pi }{{\int_{0}^{\pi }{{\frac{{32}}{5}{{\sin }^3}\varphi \,d\theta }}\,d\varphi }}\end{align*}\] Show Step 5Next let’s do the \(\theta \) integration.
\[\begin{align*}\iiint\limits_{E}{{{x^2} + {y^2}\,dV}} & = \int_{0}^{\pi }{{\left. {\left( {\frac{{32}}{5}\theta {{\sin }^3}\varphi } \right)} \right|_0^\pi \,d\varphi }}\\ & = \int_{0}^{\pi }{{\frac{{32}}{5}\pi {{\sin }^3}\varphi \,d\varphi }}\end{align*}\] Show Step 6Finally, we’ll do the \(\varphi \) integration.
\[\begin{align*}\iiint\limits_{E}{{{x^2} + {y^2}\,dV}} & = \int_{0}^{\pi }{{\frac{{32}}{5}\pi {{\sin }^2}\varphi \sin \varphi \,d\varphi }}\\ & = \int_{0}^{\pi }{{\frac{{32}}{5}\pi \left( {1 - {{\cos }^2}\varphi } \right)\sin \varphi \,d\varphi }}\\ & = \left. {\left( { - \frac{{32}}{5}\pi \left( {\cos \varphi - \frac{1}{3}{{\cos }^3}\varphi } \right)} \right)} \right|_0^\pi = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{128}}{{15}}\pi }}\end{align*}\]You do recall how to do the kinds of trig integrals we did in this step don’t you? If not you should head back and review some of the Calculus II material as these will be showing up on occasion.
Note that, in this case, because the limits of each of the integrals were all constants we could have done the integration in any order we wanted to.