Section 15.5 : Triple Integrals
3. Evaluate \( \displaystyle \iiint\limits_{E}{{6{z^2}\,dV}}\) where \(E\) is the region below \(4x + y + 2z = 10\) in the first octant.
Show All Steps Hide All Steps
Start SolutionOkay, let’s start off with a quick sketch of the region \(E\) so we can get a feel for what we’re dealing with.
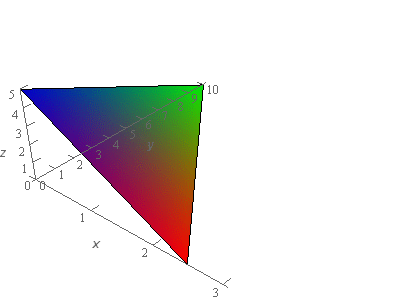
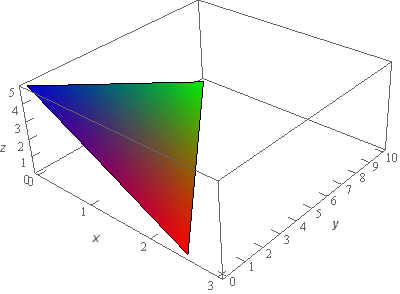
We’ve given the sketches with a set of “traditional” axes as well as a set of “box” axes to help visualize the surface and region.
For this problem the region \(E\) is just the region that is under the plane shown above and in the first octant. In other words, the sketch of the plane above is exactly the top of the region \(E\). The bottom of the region is the \(xy\)-plane while the sides are simply the \(yz\) and \(xz\)-planes.
Show Step 2So, from the sketch above we know that we’ll have the following limits for \(z\).
\[0 \le z \le 5 - 2x - \frac{1}{2}y\]where we got the upper \(z\) limit simply by solving the equation of the plane for \(z\).
With these limits we can also get the triple integral at least partially set up as follows.
\[\iiint\limits_{E}{{6{z^2}\,dV}} = \iint\limits_{D}{{\left[ {\int_{0}^{{5 - 2x - \frac{1}{2}y}}{{6{z^2}\,dz}}} \right]\,dA}}\] Show Step 3Next, we’ll need limits for \(D\) so we can finish setting up the integral. For this problem \(D\) is simply the region in the \(xy\)-plane (since we are integrating with respect to \(z\) first) that we used to graph the plane in Step 1. That also, in this case, makes \(D\) the bottom of the region.
Here is a sketch of \(D\).
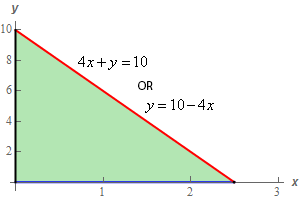
The hypotenuse of \(D\) is simply the intersection of the plane from Step 1 and the \(xy\)-plane and so we can quickly get its equation by plugging \(z = 0\) into the equation of the plane.
Given the nature of this region as well as the function we’ll be integrating it looks like we can use either order of integration for \(D\). So, to keep the limits at least a little nicer we’ll integrate \(y\)’s and then \(x\)’s.
Here are the limits for the double integral over \(D\).
\[\begin{array}{c} \displaystyle 0 \le x \le \frac{5}{2}\\ 0 \le y \le 10 - 4x\end{array}\]The upper \(x\) limit was found simply by plugging \(y = 0\) into the equation of the hypotenuse and solving for \(x\) to determine where the hypotenuse intersected the \(x\)-axis.
With these limits plugged into the integral we now have,
\[\iiint\limits_{E}{{6{z^2}\,dV}} = \int_{0}^{{\frac{5}{2}}}{{\int_{0}^{{10 - 4x}}{{\int_{0}^{{5 - 2x - \frac{1}{2}y}}{{6{z^2}\,dz}}\,dy}}\,dx}}\] Show Step 4Okay, now all we need to do is evaluate the integral. Here is the \(z\) integration.
\[\begin{align*}\iiint\limits_{E}{{6{z^2}\,dV}} & = \int_{0}^{{\frac{5}{2}}}{{\int_{0}^{{10 - 4x}}{{\left. {\left( {2{z^3}} \right)} \right|_0^{5 - 2x - \frac{1}{2}y}\,dy}}\,dx}}\\ & = \int_{0}^{{\frac{5}{2}}}{{\int_{0}^{{10 - 4x}}{{2{{\left( {5 - 2x - \frac{1}{2}y} \right)}^3}dy}}\,dx}}\end{align*}\]Do not multiply out the integrand of this integral.
Show Step 5As noted in the last step we do not want to multiply out the integrand of this integral. One of the bigger mistakes students make with multiple integrals is to just launch into a simplification mode after the integral and multiply everything out.
Sometimes of course that must be done but, in this case, note that we can easily do the \(y\) integration with a simple Calculus I substitution. Here is that work.
\[\begin{align*}\iiint\limits_{E}{{6{z^2}\,dV}} & = \int_{0}^{{\frac{5}{2}}}{{\left. { - {{\left( {5 - 2x - \frac{1}{2}y} \right)}^4}} \right|_0^{10 - 4x}\,dx}}\hspace{0.25in}\hspace{0.25in}u = 5 - 2x - \frac{1}{2}y\\ & = \int_{0}^{{\frac{5}{2}}}{{{{\left( {5 - 2x} \right)}^4}\,dx}}\end{align*}\]We gave the substitution used in this step but are leaving it to you to verify the details of the substitution.
Show Step 6Again, notice that we can either do some “simplification” or we can just do another substitution to finish this integral out. Here is the final integration step for this problem. We’ll leave it to you to verify the substitution details.
\[\begin{align*}\iiint\limits_{E}{{6{z^2}\,dV}} & = \int_{0}^{{\frac{5}{2}}}{{{{\left( {5 - 2x} \right)}^4}\,dx}}\hspace{0.25in}\hspace{0.25in}u = 5 - 2x\\ & = \left. { - \frac{1}{{10}}{{\left( {5 - 2x} \right)}^5}} \right|_0^{\frac{5}{2}}\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{625}}{2}}}\end{align*}\]So, once we got the limits all set up, the integration for this problem wasn’t too bad provided we took advantage of the substitutions of course. That will often be the case with these problems. Getting the limits for the integrals set up will often, but not always, be the hardest part of the problem. Once they get set up the integration is often pretty simple.
Also, as noted above do not forget about your basic Calculus I substitutions. Using them will often allow us to avoid some messy algebra that will be easy to make a mistake with.