Section 4.3 : Minimum and Maximum Values
3. Sketch the graph of \(g\left( x \right) = {x^2} - 4x\) and identify all the relative extrema and absolute extrema of the function on each of the following intervals.
- \(\left( { - \infty ,\infty } \right)\)
- \(\left[ { - 1,4} \right]\)
- \(\left[ {1,3} \right]\)
- \(\left[ {3,5} \right]\)
- \(\left( { - 1,5} \right]\)
Show All Solutions Hide All Solutions
a \(\left( { - \infty ,\infty } \right)\) Show SolutionHere’s a graph of the function on the interval.
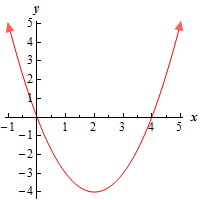
If you don’t recall how to graph parabolas you should check out the section on graphing parabolas in the Algebra notes.
So, on the interval \(\left( { - \infty ,\infty } \right)\), we can clearly see that there are no absolute maximums (the graph increases without bounds on both the left and right side of the graph.). There are also no relative maximums (there are no “bumps” in which the graph is a maximum in the region around the point). The point \(\left( {2, - 4} \right)\) is both a relative minimum and an absolute minimum.
b \(\left[ { - 1,4} \right]\) Show Solution
Here’s a graph of the function on this interval.
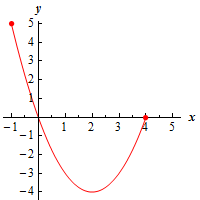
The point \(\left( {2, - 4} \right)\) is still both a relative minimum and an absolute minimum. There are still no relative maximums. However, because we are now working on a closed interval (i.e. we are working on an interval with finite endpoints and we are including the endpoints) we can see that we have an absolute maximum at the point \(\left( { - 1,5} \right)\).
c \(\left[ {1,3} \right]\) Show Solution
Here’s a graph of the function on this interval.
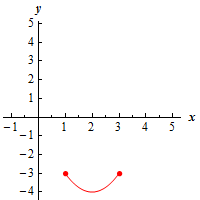
The point \(\left( {2, - 4} \right)\) is still both a relative minimum and an absolute minimum. There are still no relative maximums of the function on this interval. However, because we are now working on a closed interval (i.e. we are working on an interval with finite endpoints and we are including the endpoints) we can see that we have an absolute maximum that occurs at the points \(\left( {1, - 3} \right)\) and \(\left( {3, - 3} \right)\).
Recall that while there can only be one absolute maximum value of a function (or minimum value if that is the case) it can occur at more than one point.
d \(\left[ {3,5} \right]\) Show Solution
Here’s a graph of the function on this interval.
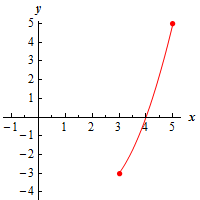
On this interval we clearly do not have any “bumps” in the interior of the interval and so, for this interval, there are no relative extrema of the function on this interval. However, we are working on a closed interval and so we can clearly see that there is an absolute maximum at the point \(\left( {5,5} \right)\) and an absolute minimum at the point \(\left( {3, - 3} \right)\).
e \(\left( { - 1,5} \right]\) Show Solution
Here’s a graph of the function on this interval.
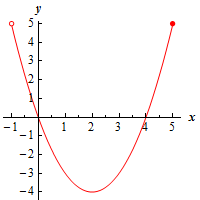
The point \(\left( {2, - 4} \right)\) is both a relative minimum and an absolute minimum. There are no relative maximums of the function on this interval.
For the absolute maximum we need to be a little careful however. In this case we are including the right endpoint of the interval, but not the left endpoint. Therefore, there is an absolute maximum at the point \(\left( {5,5} \right)\). There is not, however, an absolute maximum at the left point because that point is not being included in the interval.
Because we are not including the left endpoint in the interval and so \(x\) will get closer and closer to \(x = - 1\) without actually reaching \(x = - 1\). This means that while the graph will get closer and closer to \(y = 5\) it will never actually reach \(y = 5\) and so there will not be an absolute maximum at the left end point.