Section 4.3 : Minimum and Maximum Values
4. Sketch the graph of \(h\left( x \right) = - {\left( {x + 4} \right)^3}\)and identify all the relative extrema and absolute extrema of the function on each of the following intervals.
- \(\left( { - \infty ,\infty } \right)\)
- \(\left[ { - 5.5, - 2} \right]\)
- \(\left[ { - 4, - 3} \right)\)
- \(\left[ { - 4, - 3} \right]\)
Show All Solutions Hide All Solutions
a \(\left( { - \infty ,\infty } \right)\) Show SolutionHere’s a graph of the function on the interval.
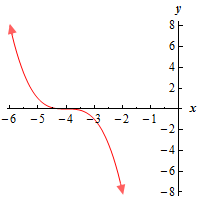
To graph this recall the transformations of graphs. The “-” in front simply reflects the graph of \({x^3}\) about the \(x\)-axis and the “+4” shifts that graph 4 units to the left.
So, on the interval \(\left( { - \infty ,\infty } \right)\), we can clearly see that there are no absolute extrema (the graph increases/decreases without bounds on both the left/right side of the graph.). There are also no relative extrema (there are no “bumps” in which the graph is a maximum or minimum in the region around the point).
Don’t get so locked into functions having to have extrema of some kind. There are all sorts of graphs that do not have absolute or relative extrema. This is one of those.
b \(\left[ { - 5.5, - 2} \right]\) Show Solution
Here’s a graph of the function on this interval.
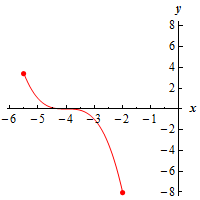
As with the first part we still have no relative extrema. However, because we are now working on a closed interval (i.e. we are working on an interval with finite endpoints and we are including the endpoints) we can see that we will have absolute extrema in the interval.
We will have an absolute maximum at the point \(\left( { - 5.5,\,\,\,3.375} \right)\) and an absolute minimum at the point \(\left( { - 2, - 8} \right)\).
c \(\left[ { - 4, - 3} \right)\) Show Solution
Here’s a graph of the function on this interval.
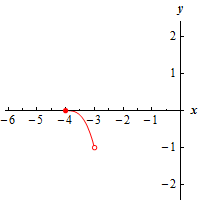
We still have no relative extrema for this function.
Because we are including the left endpoint in the interval we can see that we have an absolute maximum at the point \(\left( { - 4,0} \right)\).
We need to be careful with the right endpoint however. It may look like we have an absolute minimum at that point, but we don’t. We are not including \(x = - 3\) in our interval. What this means is that we are going to continue to take values of \(x\) that are closer and closer to \(x = - 3\) and graphing them, but we aren’t going to ever reach \(x = - 3\). Therefore, technically, the graph will continually decreases without ever actually reaching a final value. It will get closer and closer to -1, but will never actually reach that point. What this means for us is that there will be no absolute minimum of the function on the given interval.
d \(\left[ { - 4, - 3} \right]\) Show Solution
Here is a graph of the function on this interval.
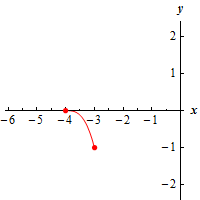
Note that the only difference between this part and the previous part is that we are now including the right endpoint in the interval. Because of that most of the answers here are identical to part (c).
There are no relative extrema of the function on the interval and there is an absolute maximum at the point \(\left( { - 4,0} \right)\).
Now, unlike part (c) we are including \(x = - 3\) in the interval and so the graph will reach a final point, so to speak, as we move to the right. Therefore, for this interval, we have an absolute minimum at the point \(\left( { - 3, - 1} \right)\).