Section 4.3 : Minimum and Maximum Values
5. Sketch the graph of some function on the interval \(\left[ {1,6} \right]\) that has an absolute maximum at \(x = 6\) and an absolute minimum at \(x = 3\).
Show All Steps Hide All Steps
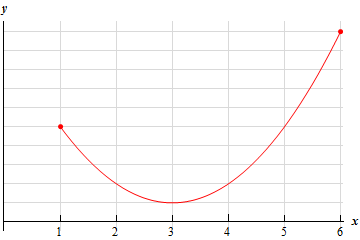
So, we need a graph of some function (not the function itself, only the graph). The graph must be on the interval \(\left[ {1,6} \right]\) and must have absolute extrema at the specified points.
By this point we should have seen enough sketches of graphs to have a pretty good idea of what absolute minimums that are not at the endpoints of an interval should look like on a graph. Therefore, we should know basically what the graph should look like at \(x = 3\).
Next, we know that the absolute maximum must occur at the right end point of the interval and so all we need to do is sketch a curve from the absolute minimum up to the right endpoint and make sure that the graph at the right endpoint is simply higher than every other point on the graph.
For the graph to the left of the absolute minimum we can sketch in pretty much anything until we reach the left end point, we just need to make sure that no portion of it goes below the absolute minimum or above the absolute maximum.
Show Step 2There are literally an infinite number of graphs that we could do here. Some will be more complicated that others, but here is probably one of the simpler graphs that we could use here.