I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 4.3 : Minimum and Maximum Values
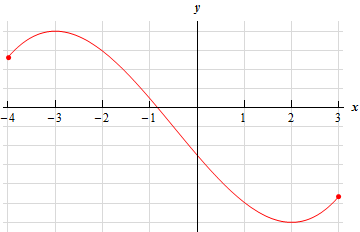
6. Sketch the graph of some function on the interval \(\left[ { - 4,3} \right]\) that has an absolute maximum at \(x = - 3\) and an absolute minimum at \(x = 2\).
Show All Steps Hide All Steps
So, we need a graph of some function (not the function itself, only the graph). The graph must be on the interval \(\left[ { - 4,3} \right]\) and must have absolute extrema at the specified points.
By this point we should have seen enough sketches of graphs to have a pretty good idea of what absolute maximums/minimums that are not at the endpoints of an interval should look like on a graph. Therefore, we should know basically what the graph should look like at \(x = - 3\) and \(x = 2\). There are many ways we could sketch the graph between these two points, but there is no reason to overly complicate the graph so the best thing to do is probably just sketch in a short smooth curve connecting the two points.
Also, because the absolute extrema occur interior to the interval we know that the graph at the endpoints of the interval must fall somewhere between the maximum/minimum values of the graph. This means that as we sketch the graph from the absolute maximum to the left end point we can sketch anything we just need to make sure it never rises above the highest point on the graph or below the lowest point on the graph.
Similarly, as we sketch the graph from the absolute minimum to the right endpoint we just need to make sure it stays between the highest and lowest point on the graph.
Show Step 2There are literally an infinite number of graphs that we could do here. Some will be more complicated that others, but here is probably one of the simpler graphs that we could use here.