Section 15.3 : Double Integrals over General Regions
15. Use a double integral to determine the volume of the region formed by the intersection of the two cylinders \({x^2} + {y^2} = 4\) and \({x^2} + {z^2} = 4\).
Show All Steps Hide All Steps
Start SolutionOkay, probably one of the hardest parts of this problem is the visualization of just what this surface looks like so let’s start with that.
First, \({x^2} + {y^2} = 4\) is a cylinder of radius 2 centered on the \(z\)-axis and \({x^2} + {z^2} = 4\) is a cylinder of radius 2 centered on the \(y\)-axis and so we will have an intersection of the two around the origin. Here is a sketch of the two cylinders.

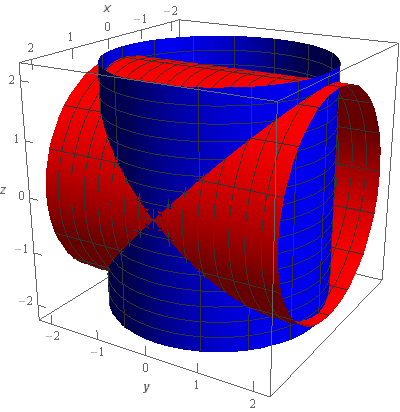
As usual we gave two sketches with different axes systems to help visualize the two cylinders.
Now, the solid we want the volume of is the portion of the red cylinder that lies inside the blue cylinder, or equivalently the portion of the blue cylinder that lies inside the red cylinder. Here are a couple of sketches of only the solid that we are after.

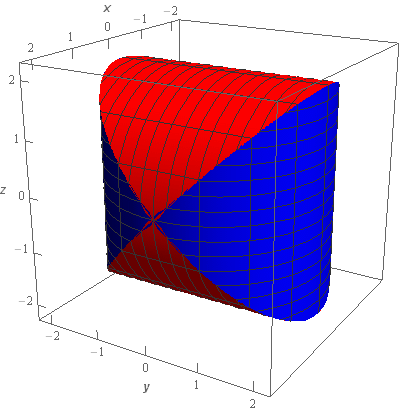
The red portion of this solid is the portion of \({x^2} + {z^2} = 4\) that lies inside \({x^2} + {y^2} = 4\) and the blue portion of this solid is the portion of \({x^2} + {y^2} = 4\) that lies inside \({x^2} + {z^2} = 4\).
Show Step 2Now we need to determine an integral that will give the volume of this solid. In this section we really only talked about finding the solid that was under a surface and above a region \(D\) in the \(xy\)-plane.
This solid also exists below the \(xy\)-plane. For this solid, however, this an easy situation to deal with. Recall that the solid is a portion of the cylinder \({x^2} + {y^2} = 4\) that is inside the cylinder \({x^2} + {z^2} = 4\), which is centered on the \(z\)‑axis. This means that the portion of the solid that is below the \(xy\)-plane is a simply a mirror image of the portion of the solid that is above the \(xy\)-plane. In other words, the volume of the portion of the solid that lies below the \(xy\)-plane is the same as the volume of the portion of the solid that lies above the \(xy\)-plane.
We can use the ideas from this section to easily find the volume of the solid above the \(xy\)‑plane and then the volume of the full solid will simply be double this.
Show Step 3So, now we need to actually set up the integral for the volume. First, we can solve \({x^2} + {z^2} = 4\) for \(z\) to get,
\[z = \pm \sqrt {4 - {x^2}} \]The positive portion of this is the equation for the top half of the cylinder centered on the \(y\)-axis and the negative portion is the equation for the bottom half of this cylinder.
This means that the integral for the volume of the top half of the solid is,
\[V = \iint\limits_{D}{{\sqrt {4 - {x^2}} \,dA}}\]The volume of the whole solid is then,
\[V = 2\iint\limits_{D}{{\sqrt {4 - {x^2}} \,dA}}\] Show Step 4Now, we need to figure out just what the region \(D\) is. We know that, in general, \(D\) is the region of the \(xy\)-plane that we use to get the graph of the surface we are working with, \(z = \sqrt {4 - {x^2}} \), in this case.
But just what is that for this problem? Look at the solid from directly above it. What you see is the following,
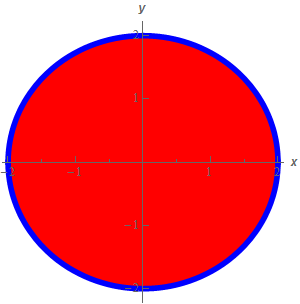
The blue circle is the cylinder \({x^2} + {y^2} = 4\) that is centered on the \(z\)-axis. Since we are looking at the solid from directly above all we see is the walls of the cylinder which of course is just a circle with equation \({x^2} + {y^2} = 4\). The red portion of this is the walls of the cylinder \({x^2} + {z^2} = 4\) that lies inside \({x^2} + {y^2} = 4\).
This is exactly what we need to determine \(D\). Recall once again that \(D\) is the region in the \(xy\)-plane we use to graph the upper portion of the surface defining the solid. But from our graph above we see that the upper portion of the surface appears to be a circle of radius 2 centered at the origin. This means that is exactly what \(D\) is. \(D\) is just shape that we see when we look at the region from above and so \(D\) is the circle shown in the graph above.
Show Step 5Next let’s get the limits for our integral. The region \(D\) itself doesn’t really seem to affect the order of integration and each set of limits are pretty much the same. The only real difference is the \(x\)’s and \(y\)’s will be switched around.
Here are the limits for each order of integration.
\[\begin{array}{*{20}{c}}\begin{array}{c} - 2 \le x \le 2\\ - \sqrt {4 - {x^2}} \le y \le \sqrt {4 - {x^2}} \end{array}&{\hspace{0.25in}{\mbox{OR}}\hspace{0.25in}}&\begin{array}{c}- 2 \le y \le 2\\ - \sqrt {4 - {y^2}} \le x \le \sqrt {4 - {y^2}} \end{array}\end{array}\]So, as noted above there doesn’t appear to be much difference in the limits. However, go back and check the integral we need to compute. We can see that if we integrate \(x\) first we’ll need to do a trig substitution. So, let’s integrate \(y\) first.
The integral for the volume of the full solid is then,
\[V = 2\iint\limits_{D}{{\sqrt {4 - {x^2}} \,dA}} = 2\int_{{ - 2}}^{2}{{\int_{{ - \sqrt {4 - {x^2}} }}^{{\sqrt {4 - {x^2}} }}{{\sqrt {4 - {x^2}} \,dy}}\,dx}}\] Show Step 6Now all we need to do is evaluate the integral. Here is the \(y\) integration.
\[\begin{align*}V & = 2\iint\limits_{D}{{\sqrt {4 - {x^2}} \,dA}} = 2\int_{{ - 2}}^{2}{{\left. {\left( {y\sqrt {4 - {x^2}} } \right)} \right|_{ - \sqrt {4 - {x^2}} }^{\sqrt {4 - {x^2}} }\,dx}}\\ & = 2\int_{{ - 2}}^{2}{{\left( {\sqrt {4 - {x^2}} - \left( { - \sqrt {4 - {x^2}} } \right)} \right)\sqrt {4 - {x^2}} \,dx}}\\ & = 2\int_{{ - 2}}^{2}{{2\sqrt {4 - {x^2}} \sqrt {4 - {x^2}} \,dx}}\\ & = 2\int_{{ - 2}}^{2}{{2\left( {4 - {x^2}} \right)\,dx}} = 4\int_{{ - 2}}^{2}{{4 - {x^2}\,dx}}\end{align*}\]We put a few more steps into the work that absolutely necessary to make the simplifications clear.
Show Step 7Finally, the \(x\) integration and hence the volume of the full solid is,
\[V = 4\int_{{ - 2}}^{2}{{4 - {x^2}\,dx}}\left. { = 4\left( {4x - \frac{1}{3}{x^3}} \right)} \right|_{ - 2}^2 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{128}}{3}}}\]So, as we can see the integration portion of the problem was surprisingly simple. The biggest issue here really is just getting this problem set up.
This problem illustrates one of the biggest issues that many students have with some of these problems. You really need to be able to visualize the solids/regions that are being dealt with. Or at the very least have the ability to get the graph of the solid/region. Unfortunately, that is not always something that can be quickly taught. Many folks just seem to naturally be able to visualize these kinds of things but many also are just not able to easily visualize them. If you are in the second set of folks it will make some of these problems a little harder unfortunately but if you persevere you will get through this stuff and hopefully start to be able to do some of the visualization that will be needed on occasion.