Section 15.3 : Double Integrals over General Regions
14. Use a double integral to determine the volume of the region bounded by \(z = 6 - 5{x^2}\) and the planes \(y = 2x\), \(y = 2\),\(x = 0\) and the \(xy\)-plane.
Show All Steps Hide All Steps
Start SolutionLet’s first get a sketch of the solid that we’re working with. If you are not good at visualizing these types of solids in your head these graphs can be invaluable in helping to get the integral set up.
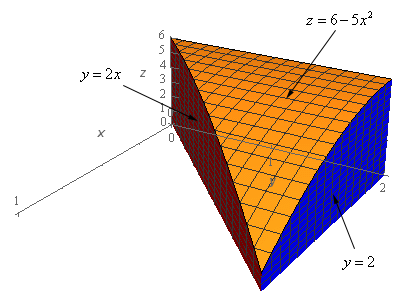
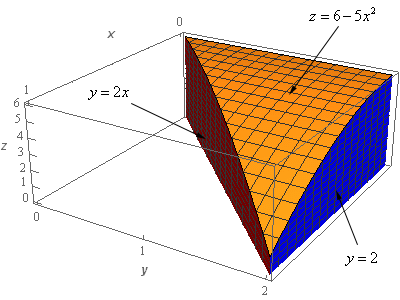
The surface is sketched with a traditional set of axes and well as a “box frame” set of axes. Sometimes it is easier to see what is going on with the surface when both sketches are present.
The upper surface (the orange surface) is the graph of \(z = 6 - 5{x^2}\). The blue plane is the graph of \(y = 2\) which is nothing more than the plane parallel to the \(xz\)-plane at \(y = 2\). The red plane is the graph of \(y = 2x\) and this is simply the plane that is perpendicular to the \(xy\)-plane and goes through the line \(y = 2x\) in the \(xy\)-plane. The surface given by \(x = 0\) is simply the \(yz\)-plane (i.e the back of the solid) and is not shown and the \(xy\)-plane is the bottom of the surface and again is not shown in the sketch.
Show Step 2In this section the only method that we have for determining the volume of a solid is to find the volume under a surface. In this case it is hopefully clear that we are looking for the surface that is under \(z = 6 - 5{x^2}\) and is above the region \(D\) in the \(xy\)-plane defined by where the other three planes intersect it. In other words, the region \(D\) is the regoin in the \(xy\)-plane that is bounded by \(y = 2\), \(y = 2x\) and \(x = 0\).
The integral for the volume is then,
\[V = \iint\limits_{D}{{6 - 5{x^2}\,dA}}\]where \(D\) is sketched below.
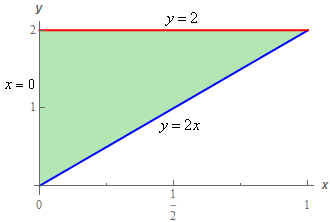
This integral can be integrated in any order so let’s integrate with respect to \(y\) first to avoid fractions in the limits (which we’d get with one if we integrated with respect to \(x\) first). Here are the limits for our integral.
\[\begin{array}{c}0 \le x \le 1\\ 2x \le y \le 2\end{array}\]The integral for the volume is then,
\[V = \iint\limits_{D}{{6 - 5{x^2}\,dA}} = \int_{0}^{1}{{\int_{{2x}}^{2}{{6 - 5{x^2}\,dy}}\,dx}}\] Show Step 4Now all we need to do is evaluate the integral. Here is the \(y\) integration.
\[V = \int_{0}^{1}{{\left( {6 - 5{x^2}} \right)\left. y \right|_{2x}^2\,dx}} = \int_{0}^{1}{{\left( {6 - 5{x^2}} \right)\left( {2 - 2x} \right)\,dx}} = \int_{0}^{1}{{10{x^3} - 10{x^2} - 12x + 12\,dx}}\]Note that in doing the \(y\) integration we acknowledged that the whole integrand contained no \(y\)’s and so could be considered a constant and so would just be multiplied by \(y\). We could also have done each term individually but sometimes it is just as easy or even easier to do what we’ve done here. Of course, we then had to multiply out the integrand for the next step but it wasn’t too bad.
Show Step 5Finally, the \(x\) integration and hence the volume is,
\[V\left. { = \left( {\frac{5}{2}{x^4} - \frac{{10}}{3}{x^3} - 6{x^2} + 12x} \right)} \right|_0^1 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{31}}{6}}}\]