Calculus III - Double Integrals over General Regions

Section 15.3 : Double Integrals over General Regions

13. Use a double integral to determine the volume of the region that is between the $xy$‑plane and$f\left( {x,y} \right) = 2 + \cos \left( {{x^2}} \right)$ and is above the triangle with vertices $\left( {0,0} \right)$, $\left( {6,0} \right)$ and $\left( {6,2} \right)$.

Show All Steps Hide All Steps

Start Solution

Let’s first get a sketch of the function and the triangle that lies under it.

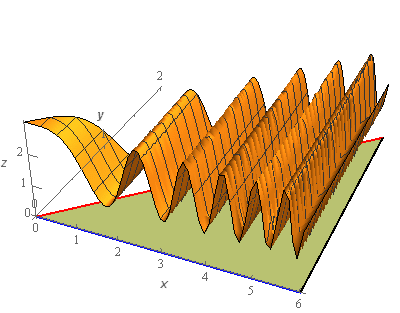
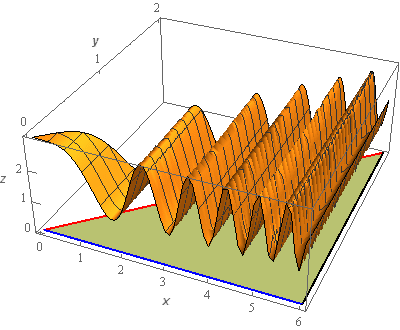
$A three dimensional sketch of the surface $f\left( {x,y} \right) = 2 + \cos \left( {{x^2}} \right)$ drawn with the traditional axes. The surface ripples up and down in the x direction with the ripples getting closer and closer together as $x$ increases, and it is constant in the y direction. The greenish triangle drawn underneath the surface on the xy-plane is the triangle with vertices $\left( {0,0} \right)$, $\left( {6,0} \right)$ and $\left( {6,2} \right)$.$

$A three dimensional sketch of the same surface $f\left( {x,y} \right) = 2 + \cos \left( {{x^2}} \right)$ and the triangle beneath it, this time drawn with a “box frame” set of axes to make the surface easier to see.$

The surface is sketched with a traditional set of axes and well as a “box frame” set of axes. Sometimes it is easier to see what is going on with the surface when both sketches are present.

The greenish triangle underneath the surface is the triangle referenced in the problem statement.

Show Step 2

Now, the volume we are after is given by the following integral,

\[V = \iint\limits_{D}{{2 + \cos \left( {{x^2}} \right)\,dA}}\]

where $D$ is the triangle referenced in the problem statement.

So, in order to evaluate the integral we’ll need a sketch of $D$ so we can determine an order of integration as well as limits for the integrals.

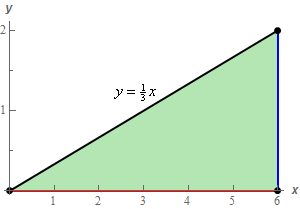
$A sketch of the region $D$. It is the triangle with vertices $\left( {0,0} \right)$, $\left( {6,0} \right)$ and $\left( {6,2} \right)$, with the bottom side along the x-axis, the right side vertical at $x = 6$ and the upper side the line $y = \frac{1}{3}x$. The inside is shaded green.$

Show Step 3

The region $D$ can easily be described for either order of integration. However, it should be pretty clear that the integral can’t be integrated with respect to $x$ first and so we’ll need to integrate with respect to $y$ first.

Here are the limits for the integral with this order.

\[\begin{array}{c} 0 \le x \le 6\\ 0 \le y \le \displaystyle \frac{1}{3}x\end{array}\]

The integral for the volume is then,

\[V = \iint\limits_{D}{{2 + \cos \left( {{x^2}} \right)\,dA}} = \int_{0}^{6}{{\int_{0}^{{\frac{1}{3}x}}{{2 + \cos \left( {{x^2}} \right)\,dy}}\,dx}}\]

Show Step 4

Now all we need to do is evaluate the integral. Here is the $y$ integration.

\[V = \int_{0}^{6}{{\left. {\left( {2y + y\cos \left( {{x^2}} \right)} \right)} \right|_0^{\frac{1}{3}x}\,dx}} = \int_{0}^{6}{{\frac{2}{3}x + \frac{1}{3}x\cos \left( {{x^2}} \right)\,dx}}\]

Show Step 5

Finally, the $x$ integration and hence the volume is,

\[V = \left. {\left( {\frac{1}{3}{x^2} + \frac{1}{6}\sin \left( {{x^2}} \right)\,} \right)} \right|_0^6 = \require{bbox} \bbox[2pt,border:1px solid black]{{12 + \frac{1}{6}\sin \left( {36} \right) = 11.8347}}\]

Don’t forget to have your calculator set to radians if you are converting to decimals!