Section 15.3 : Double Integrals over General Regions
12. Use a double integral to determine the area of the region bounded by \(y = 1 - {x^2}\) and \(y = {x^2} - 3\).
Show All Steps Hide All Steps
Start SolutionOkay, we know that the area of any region \(D\) can be found by evaluating the following double integral.
\[A = \iint\limits_{D}{{dA}}\]For this problem \(D\) is the region sketched below.
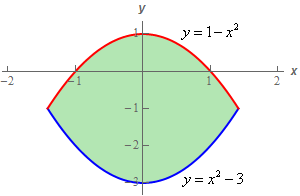
We’ve done enough double integrals by this point that it should be pretty obvious the best order of integration is to integrate with respect to \(y\) first.
Here are the limits for the integral with this order.
\[\begin{array}{c} - \sqrt 2 \le x \le \sqrt 2 \\ {x^2} - 3 \le y \le 1 - {x^2}\end{array}\]The \(x\) limits can easily be found by setting the two equations equal and solving for \(x\).
Show Step 3The integral for the area is then,
\[A = \iint\limits_{D}{{dA}} = \int_{{ - \sqrt 2 }}^{{\sqrt 2 }}{{\int_{{{x^2} - 3}}^{{1 - {x^2}}}{{\,dy}}\,dx}}\] Show Step 4Now all we need to do is evaluate the integral. Here is the \(y\) integration.
\[A = \iint\limits_{D}{{dA}} = \int_{{ - \sqrt 2 }}^{{\sqrt 2 }}{{\left. y \right|_{{x^3} - 3}^{1 - {x^2}}\,dx}} = \int_{{ - \sqrt 2 }}^{{\sqrt 2 }}{{4 - 2{x^2}\,dx}}\] Show Step 5Finally, the \(x\) integration and hence the area of \(D\) is,
\[A = \left. {\left( {4x - \frac{2}{3}{x^3}} \right)} \right|_{ - \sqrt 2 }^{\sqrt 2 } = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{16\sqrt 2 }}{3}}}\]