Calculus III - Double Integrals over General Regions

Hide Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 15.3 : Double Integrals over General Regions

Back to Problem List

11. Evaluate $\displaystyle \int_{0}^{1}{{\int_{{ - \sqrt y }}^{{{y^{\,2}}}}{{6x - y\,dx}}\,dy}}$ by first reversing the order of integration.

Show All Steps Hide All Steps

Start Solution

Note that with this problem, unlike the previous problem, there is no issues with this order of integration. We could easily do this integral in the given order. We are only reversing the order in the problem because we were told to do so in the problem statement.

Here are the limits we get from the integral.

$\begin{array}{c}0 \le y \le 1\\ - \sqrt y \le x \le {y^2}\end{array}$

Here is a quick sketch of the region these limits describe.

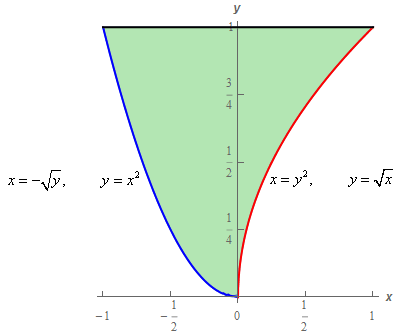
When reversing the order of integration it is often very helpful to have a sketch of the region to make sure we get the correct limits for the reversed order. That is especially the case with this problem.

Show Step 2

Okay, if we reverse the order of integration we need to integrate with respect to $y$ first. That leads to a small issue however. The lower function changes and so we’ll need to split this up into two regions which in turn will mean two integrals when we reverse the order integration.

The limits for each of the regions with the reversed order are then,

$\begin{array}{*{20}{c}}\begin{array}{c} - 1 \le x \le 0\\ \,{x^2} \le y \le 1\end{array}&{\hspace{0.5in}}&\begin{array}{c}0 \le x \le 1\\ \sqrt x \le y \le 1\end{array}\end{array}$

The integrals with reversed order are then,

$\int_{0}^{1}{{\int_{{ - \sqrt y }}^{{{y^{\,2}}}}{{6x - y\,dx}}\,dy}} = \int_{{ - 1}}^{0}{{\int_{{{x^2}}}^{1}{{6x - y\,dy}}\,dx}} + \int_{0}^{1}{{\int_{{\sqrt x }}^{1}{{6x - y\,dy}}\,dx}}$ Show Step 3

Now all we need to do is evaluate the integrals. Here is the $y$ integration for each.

$\begin{align*}\int_{0}^{1}{{\int_{{ - \sqrt y }}^{{{y^{\,2}}}}{{6x - y\,dx}}\,dy}} & = \int_{{ - 1}}^{0}{{\left. {\left( {6xy - \frac{1}{2}{y^2}} \right)} \right|_{{x^2}}^1\,dx}} + \int_{0}^{1}{{\left. {\left( {6xy - \frac{1}{2}{y^2}} \right)} \right|_{\sqrt x }^1\,dx}}\\ & = \int_{{ - 1}}^{0}{{\frac{1}{2}{x^4} - 6{x^3} + 6x - \frac{1}{2}\,dx}} + \int_{0}^{1}{{ - 6{x^{\frac{3}{2}}} + \frac{{13}}{2}x - \frac{1}{2}\,dx}}\end{align*}$ Show Step 4

Finally, the $x$ integration.

$\begin{align*}\int_{0}^{1}{{\int_{{ - \sqrt y }}^{{{y^{\,2}}}}{{6x - y\,dx}}\,dy}} & = \left. {\left( {\frac{1}{{10}}{x^5} - \frac{3}{2}{x^4} + 3{x^2} - \frac{1}{2}x} \right)} \right|_{ - 1}^0 + \left. {\left( { - \frac{{12}}{5}{x^{\frac{5}{2}}} + \frac{{13}}{4}{x^2} - \frac{1}{2}x} \right)} \right|_0^1\\ & = \hspace{1.0in} - \frac{{19}}{{10}}\hspace{1.15in} + \hspace{1.0in}\frac{7}{{20}}\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{ - \frac{{31}}{{20}}}}\end{align*}$