Calculus III - Double Integrals over General Regions

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 15.3 : Double Integrals over General Regions

Back to Problem List

10. Evaluate \(\displaystyle \int_{0}^{3}{{\int_{{2x}}^{6}{{\sqrt {{y^2} + 2} \,dy}}\,dx}}\) by first reversing the order of integration.

Show All Steps Hide All Steps

Start Solution

Let’s start off by noticing that if we were to integrate with respect to \(y\) first we’d need to do a trig substitution (which we’ll all be thankful if we don’t need to do it!) so interchanging the order in this case might well save us a messy integral.

So, here are the limits we get from the integral.

\[\begin{array}{c}0 \le x \le 3\\ 2x \le y \le 6\end{array}\]

Here is a quick sketch of the region these limits describe.

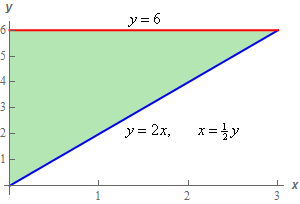
When reversing the order of integration it is often very helpful to have a sketch of the region to make sure we get the correct limits for the reversed order.

Show Step 2

Okay, if to reverse the order of integration we need to integrate with respect to \(x\) first. The limits for the reversed order are then,

\[\begin{array}{c}0 \le y \le 6\\ 0 \le x \displaystyle \le \frac{1}{2}y\end{array}\]

The integral with reversed order is,

\[\int_{0}^{3}{{\int_{{2x}}^{6}{{\sqrt {{y^2} + 2} \,dy}}\,dx}} = \int_{0}^{6}{{\int_{0}^{{\frac{1}{2}y}}{{\sqrt {{y^2} + 2} \,dx}}\,dy}}\] Show Step 3

Now all we need to do is evaluate the integrals. Here is the \(x\) integration.

\[\int_{0}^{3}{{\int_{{2x}}^{6}{{\sqrt {{y^2} + 2} \,dy}}\,dx}} = \int_{0}^{6}{{\left. {\left( {x\sqrt {{y^2} + 2} } \right)} \right|_0^{\frac{1}{2}y}\,dy}} = \int_{0}^{6}{{\frac{1}{2}y\sqrt {{y^2} + 2} \,dy}}\] Show Step 4

Note that because of the \(x\) integration we’ll not need to do a trig substitution. All we need is a simple Calculus I integral. Here is the \(y\) integration (we’ll leave it to you to verify the substitution details).

\[\int_{0}^{3}{{\int_{{2x}}^{6}{{\sqrt {{y^2} + 2} \,dy}}\,dx}} = \left. {\left( {\frac{1}{6}{{\left( {{y^2} + 2} \right)}^{\frac{3}{2}}}} \right)} \right|_0^6 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{1}{6}\left( {{{38}^{\frac{3}{2}}} - {2^{\frac{3}{2}}}} \right) = 38.5699}}\]