Calculus III - Double Integrals over General Regions

Hide Mobile Notice

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 15.3 : Double Integrals over General Regions

Back to Problem List

9. Evaluate $\displaystyle \iint\limits_{D}{{7{x^2} + 14y\,dA}}$ where $D$ is the region bounded by $x = 2{y^2}$ and $x = 8$ in the order given below.

Integrate with respect to $x$ first and then $y$ .
Integrate with respect to $y$ first and then $x$ .

Show All Solutions Hide All Solutions

a Integrate with respect to

$x$ first and then

$y$ . Show All Steps Hide All Steps
Start Solution

Here’s a quick sketch of the region with the curves labeled for integration with respect to $x$ first.

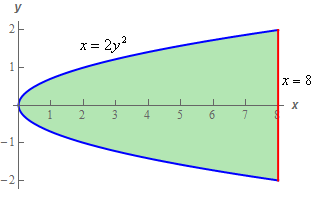
The limits for the integral for integration with respect to $x$ first are then,

$\begin{array}{c} - 2 \le y \le 2\\ \,2{y^2} \le x \le 8\end{array}$

Plugging these limits into the integral is then,

$\iint\limits_{D}{{7{x^2} + 14y\,dA}} = \int_{{ - 2}}^{2}{{\int_{{2{y^2}}}^{8}{{7{x^2} + 14y\,dx}}\,dy}}$ Show Step 2

The $x$ integration for this integral is,

$\begin{align*}\iint\limits_{D}{{7{x^2} + 14y\,dA}} & = \int_{{ - 2}}^{2}{{\int_{{2{y^2}}}^{8}{{7{x^2} + 14y\,dx}}\,dy}}\\ & = \int_{{ - 2}}^{2}{{\left. {\left( {\frac{7}{3}{x^3} + 14xy} \right)} \right|_{2{y^2}}^8\,dy}}\\ & = \int_{{ - 2}}^{2}{{\frac{{3584}}{3} + 112y - 28{y^3} - \frac{{56}}{3}{y^6}\,dy}}\end{align*}$ Show Step 3

Finally, the $y$ integration is,

$\begin{align*}\iint\limits_{D}{{7{x^2} + 14y\,dA}} & = \int_{{ - 2}}^{2}{{\frac{{3584}}{3} + 112y - 28{y^3} - \frac{{56}}{3}{y^6}\,dy}}\\ & = \left. {\left( {\frac{{3584}}{3}y + 56{y^2} - 7{y^4} - \frac{8}{3}{y^7}} \right)} \right|_{ - 2}^2 = \require{bbox} \bbox[2pt,border:1px solid black]{{4096}}\end{align*}$

b Integrate with respect to

$y$ first and then

$x$ . Show All Steps Hide All Steps
Start Solution

Here’s a quick sketch of the region with the curves labeled for integration with respect to $y$ first.

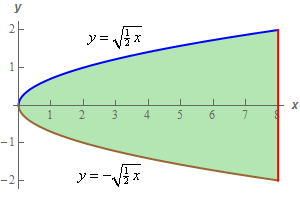
Note that in order to do $y$ integration first we needed to solve the equation of the parabola for $y$ so the top and bottom curve will have distinct equations in terms of $x$ , which we need to integrate with respect to $y$ first.

The limits for the integral for integration with respect to $y$ first are then,

$\begin{array}{c} \displaystyle 0 \le x \le 8\\ - \sqrt {\frac{1}{2}x} \le y \le \sqrt {\frac{1}{2}x} \end{array}$

Plugging these limits into the integral is then,

$\iint\limits_{D}{{7{x^2} + 14y\,dA}} = \int_{0}^{8}{{\int_{{ - \sqrt {\frac{1}{2}x} }}^{{\sqrt {\frac{1}{2}x} }}{{7{x^2} + 14y\,dy}}\,dx}}$ Show Step 2

The $y$ integration for this integral is,

$\begin{align*}\iint\limits_{D}{{7{x^2} + 14y\,dA}} & = \int_{0}^{8}{{\int_{{ - \sqrt {\frac{1}{2}x} }}^{{\sqrt {\frac{1}{2}x} }}{{7{x^2} + 14y\,dy}}\,dx}}\\ & = \int_{0}^{8}{{\left. {\left( {7{x^2}y + 7{y^2}} \right)} \right|_{ - \sqrt {\frac{1}{2}x} }^{\sqrt {\frac{1}{2}x} }\,dx}}\\ & = \int_{0}^{8}{{\frac{{14}}{{\sqrt 2 }}{x^{\frac{5}{2}}}\,dx}}\end{align*}$ Show Step 3

Finally, the $x$ integration is,

$\iint\limits_{D}{{7{x^2} + 14y\,dA}} = \int_{0}^{8}{{\frac{{14}}{{\sqrt 2 }}{x^{\frac{5}{2}}}\,dx}} = \left. {\left( {\frac{4}{{\sqrt 2 }}{x^{\frac{7}{2}}}} \right)} \right|_0^8 = \require{bbox} \bbox[2pt,border:1px solid black]{{4096}}$

We got the same result as the first order of integration as we knew we would.