Section 15.3 : Double Integrals over General Regions
8. Evaluate \( \displaystyle \iint\limits_{D}{{{{\bf{e}}^{\,{y^{\,4}}}}\,dA}}\) where \(D\) is the region shown below.
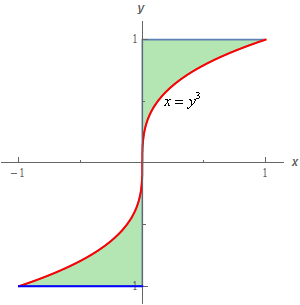
Show All Steps Hide All Steps
Start SolutionFirst, let’s label the two sub regions in \(D\) as shown below.
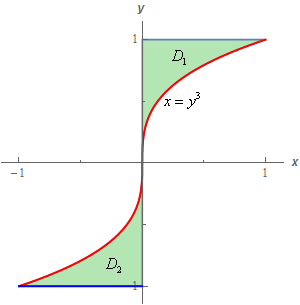
Despite the fact that each of the regions is bounded by the same curve we cannot get a single set of limits that will completely describe \(D\). In the upper region \(x = {y^3}\) is the right boundary and in the lower region \(x = {y^3}\) is the left boundary.
Therefore, each region will need a separate set of limits and so we’ll need to split the integral as follows.
\[\iint\limits_{D}{{{{\bf{e}}^{\,{y^{\,4}}}}\,dA}} = \iint\limits_{{{D_{\,1}}}}{{{{\bf{e}}^{\,{y^{\,4}}}}\,dA}} + \iint\limits_{{{D_{\,2}}}}{{{{\bf{e}}^{\,{y^{\,4}}}}\,dA}}\] Show Step 3Hopefully it is clear that we’ll need to integrate \(x\) first with both of the integrals. So, here are the limits for each integral.
\[\begin{array}{*{20}{c}}\begin{array}{c}{D_{\,1}}\\ \,0 \le y \le 1\\ 0 \le x \le {y^3}\end{array}&{\hspace{0.5in}}&\begin{array}{c}{D_{\,2}}\\ - 1 \le y \le 0\\ {y^3} \le x \le 0\end{array}\end{array}\]The integrals are then,
\[\iint\limits_{D}{{{{\bf{e}}^{\,{y^{\,4}}}}\,dA}} = \int_{0}^{1}{{\int_{0}^{{{y^3}}}{{{{\bf{e}}^{\,{y^{\,4}}}}\,dx}}\,dy}} + \int_{{ - 1}}^{0}{{\int_{{{y^3}}}^{0}{{{{\bf{e}}^{\,{y^{\,4}}}}\,dx}}\,dy}}\] Show Step 4Not much to do now other than do the integrals. Here is the \(x\) integration for both of them.
\[\begin{align*}\iint\limits_{D}{{{{\bf{e}}^{\,{y^{\,4}}}}\,dA}} & = \int_{0}^{1}{{\left. {\left( {x{{\bf{e}}^{\,{y^{\,4}}}}} \right)} \right|_0^{{y^3}}\,dy}} + \int_{{ - 1}}^{0}{{\left. {\left( {x{{\bf{e}}^{\,{y^{\,4}}}}} \right)} \right|_{{y^3}}^0\,dy}}\\ & = \int_{0}^{1}{{{y^3}{{\bf{e}}^{\,{y^{\,4}}}}\,dy}} + \int_{{ - 1}}^{0}{{ - {y^3}{{\bf{e}}^{\,{y^{\,4}}}}\,dy}}\end{align*}\] Show Step 5Finally, here is the \(y\) integration for both of the integrals.
\[\begin{align*}\iint\limits_{D}{{{{\bf{e}}^{\,{y^{\,4}}}}\,dA}} & = \int_{0}^{1}{{{y^3}{{\bf{e}}^{\,{y^{\,4}}}}\,dy}} + \int_{{ - 1}}^{0}{{ - {y^3}{{\bf{e}}^{\,{y^{\,4}}}}\,dy}}\\ & = \left. {\left( {\frac{1}{4}{{\bf{e}}^{\,{y^{\,4}}}}} \right)} \right|_0^1 + \left. {\left( { - \frac{1}{4}{{\bf{e}}^{\,{y^{\,4}}}}} \right)} \right|_{ - 1}^0\\ & = \,\frac{1}{4}\left( {{\bf{e}} - 1} \right) + \frac{1}{4}\left( { - 1 + {\bf{e}}} \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{1}{2}\left( {{\bf{e}} - 1} \right) = 0.8591}}\end{align*}\]Don’t always expect every integral over a region to be done with a single integral. On occasion you will need to split the integral up and do the actual integration over separate sub regions. In this case that was fairly obvious but sometimes it might not be so clear until you get into the problem and realize it would be easier to do over sub regions.