Section 15.3 : Double Integrals over General Regions
6. Evaluate \( \displaystyle \iint\limits_{D}{{\frac{1}{{{y^{\frac{1}{3}}}\left( {{x^3} + 1} \right)}}\,dA}}\) where \(D\) is the region bounded by \(x = - {y^{\frac{1}{3}}}\), \(x = 3\) and the \(x\)-axis.
Show All Steps Hide All Steps
Start SolutionBelow is a quick sketch of the region \(D\).
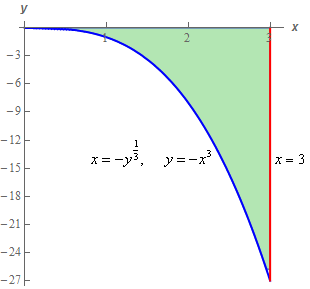
Note that we gave both forms of the equation for the left curve to help with the next step.
In general, this sketch is often important to setting the integral up correctly. We’ll need to determine the order of integration and often the region will “force” a particular order. Many regions can only be dealt with easily by doing one particular order of integration and sometimes the only way to really see that is to have a sketch of \(D\).
Even if you can do the integral in either order the sketch of \(D\) will often help with setting up the limits for the integrals.
Show Step 2Now, with this problem, the region will allow either order of integration without any real change of difficulty in the integration.
So, here are the limits for each order of integration that we could use.
\[\begin{array}{*{20}{c}}\begin{array}{c}0 \le x \le 3\\ - {x^3} \le y \le 0\end{array}&{\hspace{0.25in}{\mbox{OR}}\hspace{0.25in}}&\begin{array}{c} - 27 \le y \le 0\\ - {y^{\frac{1}{3}}} \le x \le 3\end{array}\end{array}\] Show Step 3As noted above either order could be done without much real change in difficulty. However, it looks like the limits are a little nicer if we integrate with respect to \(y\) first. One of the \(y\) limits is zero and the \(x\) limits are smaller so it looks like this might be a little easier to deal with.
So, for this problem let’s integrate with respect to \(y\) first. Here is the integral set up for \(y\) integration first.
\[\iint\limits_{D}{{\frac{1}{{{y^{\frac{1}{3}}}\left( {{x^3} + 1} \right)}}\,dA}} = \int_{0}^{3}{{\int_{{ - {x^3}}}^{0}{{\frac{1}{{{y^{\frac{1}{3}}}\left( {{x^3} + 1} \right)}}\,dy}}\,dx}}\] Show Step 4Here is the \(y\) integration.
\[\begin{align*}\iint\limits_{D}{{\frac{1}{{{y^{\frac{1}{3}}}\left( {{x^3} + 1} \right)}}\,dA}} & = \int_{0}^{3}{{\int_{{ - {x^3}}}^{0}{{\frac{1}{{{y^{\frac{1}{3}}}\left( {{x^3} + 1} \right)}}\,dy}}\,dx}}\\ & = \int_{0}^{3}{{\left. {\left( {\frac{{\frac{3}{2}{y^{\frac{2}{3}}}}}{{\left( {{x^3} + 1} \right)}}} \right)} \right|_{ - {x^3}}^0\,dx}}\\ & = \int_{0}^{3}{{ - \frac{{\frac{3}{2}{{\left( { - {x^3}} \right)}^{\frac{2}{3}}}}}{{\left( {{x^3} + 1} \right)}}\,\,dx}} = \int_{0}^{3}{{ - \frac{{\frac{3}{2}{x^2}}}{{\left( {{x^3} + 1} \right)}}\,\,dx}}\end{align*}\]Be careful with the minus signs in this integration. The minus sign in front of the integrand comes from the evaluation process (recall we first evaluate at zero!). The minus sign in the numerator will be eliminated when we deal with the exponent (the numerator of the exponent is a two so we need to square things!).
Show Step 5Now the \(x\) integration is a simple Calculus I substitution. We’ll leave the substitution work to you to verify. Here is the \(x\) integration.
\[\iint\limits_{D}{{\frac{1}{{{y^{\frac{1}{3}}}\left( {{x^3} + 1} \right)}}\,dA}} = \int_{0}^{3}{{ - \frac{{\frac{3}{2}{x^2}}}{{\left( {{x^3} + 1} \right)}}\,\,dx}} = \left. {\left( { - \frac{1}{2}\ln \left( {{x^3} + 1} \right)} \right)} \right|_0^3 = \require{bbox} \bbox[2pt,border:1px solid black]{{ - \frac{1}{2}\ln \left( {28} \right) = - 1.6661}}\]Remember that \(\ln \left( 1 \right) = 0\)!