Section 15.4 : Double Integrals in Polar Coordinates
4. Use a double integral to determine the area of the region that is inside \(r = 4 + 2\sin \theta \) and outside \(r = 3 - \sin \theta \).
Show All Steps Hide All Steps
Start SolutionBelow is a quick sketch of the region \(D\).
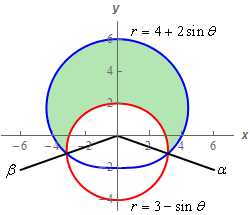
For double integrals in which polar coordinates are going to be used the sketch of \(D\) is often not as useful as for a general region.
In this case however, the sketch is probably more useful than for most of these problems. First, we can readily identify the correct order for the \(r\) limits (i.e. which is the “smaller” and which is the “larger” curve”). Secondly, it makes it clear that we are going to need to determine the limits of \(\alpha \le \theta \le \beta \) that we’ll need to do the integral.
Show Step 2So, as noted above the limits of \(r\) are (hopefully) pretty clear. To find the limits for \(\theta \) all we need to do is set the two equations equal. Doing that gives,
\[\begin{align*}4 + 2\sin \theta &= 3 - \sin \theta \\ 3\sin \theta & = - 1\\ \sin \theta & = - \frac{1}{3}\hspace{0.5in} \Rightarrow \hspace{0.5in}\theta = {\sin ^{ - 1}}\left( { - \frac{1}{3}} \right) = - 0.3398\end{align*}\]This is the angle in the fourth quadrant, i.e. \(\alpha = - 0.3398\). To find the second angle we can note that the angles that the two black lines make with the \(x\) axis are the same (ignoring the sign of course). Therefore, the second angle will simply be \(\beta = \pi + 0.3398 = 3.4814\).
The limits are then,
\[\begin{array}{c} - 0.3398 \le \theta \le 3.4814\\ 3 - \sin \theta \le r \le 4 + 2\sin \theta \end{array}\] Show Step 3We know that the following double integral will give the area of any region \(D\).
\[A = \iint\limits_{D}{{dA}}\]For our problem the region \(D\) is the region given in the problem statement and so the integral in terms of polar coordinates is then,
\[A = \iint\limits_{D}{{dA}} = \int_{{ - 0.3398}}^{{3.4814}}{{\int_{{3 - \sin \theta }}^{{4 + 2\sin \theta }}{{\,r\,dr}}\,d\theta }}\]When converting the integral don’t forget that \(dA = r\,dr\,d\theta \) and so we’ll pickup an extra \(r\) in the integrand. Forgetting the extra \(r\) is one of the most common mistakes with these kinds of problems and that seems to be even truer for area integrals such as this one.
Show Step 4Here is the \(r\) integration.
\[\begin{align*}A & = \int_{{ - 0.3398}}^{{3.4814}}{{\int_{{3 - \sin \theta }}^{{4 + 2\sin \theta }}{{\,r\,dr}}\,d\theta }}\\ & = \int_{{ - 0.3398}}^{{3.4814}}{{\left. {\frac{1}{2}{r^2}} \right|_{3 - \sin \theta }^{4 + 2\sin \theta }\,d\theta }}\\ & = \int_{{ - 0.3398}}^{{3.4814}}{{\frac{1}{2}\left[ {{{\left( {4 + 2\sin \theta } \right)}^2} - {{\left( {3 - \sin \theta } \right)}^2}} \right]\,d\theta }}\end{align*}\]Note that if you remember doing these kinds of area problems back in the Calculus II material that integral should look pretty familiar as it follows the formula we used back in that material.
Show Step 5Finally, here is the \(\theta \) integration.
\[\begin{align*}A & = \int_{{ - 0.3398}}^{{3.4814}}{{\frac{1}{2}\left[ {{{\left( {4 + 2\sin \theta } \right)}^2} - {{\left( {3 - \sin \theta } \right)}^2}} \right]\,d\theta }}\\ & = \frac{1}{2}\int_{{ - 0.3398}}^{{3.4814}}{{16 + 16\sin \theta + 4{{\sin }^2}\theta - \left( {9 - 6\sin \theta + {{\sin }^2}\theta } \right)\,d\theta }}\\ & = \frac{1}{2}\int_{{ - 0.3398}}^{{3.4814}}{{7 + 22\sin \theta + 3{{\sin }^2}\theta \,d\theta }}\\ & = \frac{1}{2}\int_{{ - 0.3398}}^{{3.4814}}{{7 + 22\sin \theta + \frac{3}{2}\left( {1 - \cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \frac{1}{2}\int_{{ - 0.3398}}^{{3.4814}}{{\frac{{17}}{2} + 22\sin \theta - \frac{3}{2}\cos \left( {2\theta } \right)\,d\theta }}\\ & = \frac{1}{2}\left. {\left( {\frac{{17}}{2}\theta - 22\cos \theta - \frac{3}{4}\sin \left( {2\theta } \right)} \right)} \right|_{ - 0.3398}^{3.4814} = \require{bbox} \bbox[2pt,border:1px solid black]{{36.5108}}\end{align*}\]There was a fair amount of simplification that needed to be done for this problem. That will often be the case. None of it was particularly difficult just tedious and easy to make a mistake if you aren’t paying attention. The “hardest” part of the simplification here was using a half angle formula to reduce the \({\sin ^2}\theta \) into something we could integrate.