Section 15.4 : Double Integrals in Polar Coordinates
5. Evaluate the following integral by first converting to an integral in polar coordinates.
\[\int_{0}^{3}{{\int_{{ - \sqrt {9 - {x^{\,2}}} }}^{0}{{\,\,\,{{\bf{e}}^{{x^{\,2}} + {y^{\,2}}}}\,dy}}\,dx}}\]Show All Steps Hide All Steps
Start SolutionThe first thing we should do here is to get a feel for the region that we are integrating over. So, here are the \(x\) and \(y\) limits of this integral.
\[\begin{array}{c}0 \le x \le 3\\ - \sqrt {9 - {x^2}} \le y \le 0\end{array}\]Now, the lower \(y\) limit tells us that the “lower” curve of the region is given by,
\[y = - \sqrt {9 - {x^2}} \hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}{x^2} + {y^2} = 9\]As noted above, if we square both sides and do a little rewrite we can see that this is a portion of a circle of radius 3 centered at the origin. In fact, it is the lower portion of the circle (because of the “-” in front of the root).
The upper \(y\) limit tells us that the region won’t go above the \(x\) axis and so the from the \(y\) limits we can see that the region is at most the lower half of the circle of radius 3 centered at the origin.
From the \(x\) limits we can see that \(x\) will never be negative and so we now know the region can’t contain any portion of the left part of the circle. The upper \(x\) limit tells us that \(x\) can go all the way out to 3.
Therefore, from the \(x\) and \(y\) limits we can see that the region we are integrating over is in fact the portion of the circle of radius 3 centered at the origin that is in the 4th quadrant. Here is a quick sketch for the sake of completeness.
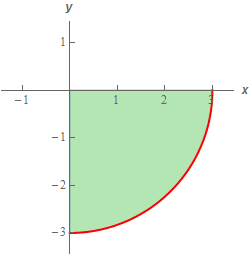
Now, we will need the polar limits for our integral and they should be pretty easy to determine from the sketch above. Here they are.
\[\begin{array}{c}\displaystyle \frac{3}{2}\pi \le \theta \le 2\pi \\ 0 \le r \le 3\end{array}\] Show Step 3Okay, we can now convert the limit to an integral involving polar coordinates. To do this just recall the various relationships between the Cartesian and polar coordinates and make use of them to convert any \(x\)’s and/or \(y\)’s into \(r\)’s and/or \(\theta \)’s.
Also, do not forget that the “dy dx” in the integral came from the \(dA\) that would have been in the original double integral (which isn’t written down but we know that it could be if we wanted to). We also know how that \(dA = r\,dr\,d\theta \) and so for this integral we will have \(dy\,dx = r\,dr\,d\theta \).
The integral is then,
\[\int_{0}^{3}{{\int_{{ - \sqrt {9 - {x^{\,2}}} }}^{0}{{\,\,\,{{\bf{e}}^{{x^{\,2}} + {y^{\,2}}}}\,dy}}\,dx}} = \int_{{\frac{3}{2}\pi }}^{{2\pi }}{{\int_{0}^{3}{{\,\,\,r{{\bf{e}}^{{r^{\,2}}}}\,dr}}\,d\theta }}\]Note that the extra \(r\) we picked up from the \(dA\) is actually needed here to make this a doable integral! It is important to not forget to properly convert the \(dA\) when converting integrals from Cartesian to polar coordinates.
Show Step 4Here is the \(r\) integration. It needs a simple substitution that we’ll leave it to you to verify the results.
\[\begin{align*}\int_{0}^{3}{{\int_{{ - \sqrt {9 - {x^{\,2}}} }}^{0}{{\,\,\,{{\bf{e}}^{{x^{\,2}} + {y^{\,2}}}}\,dy}}\,dx}} & = \int_{{\frac{3}{2}\pi }}^{{2\pi }}{{\int_{0}^{3}{{\,\,\,r{{\bf{e}}^{{r^{\,2}}}}\,dr}}\,d\theta }}\\ & = \int_{{\frac{3}{2}\pi }}^{{2\pi }}{{\left. {\frac{1}{2}{{\bf{e}}^{{r^{\,2}}}}} \right|_0^3\,d\theta }}\\ & = \int_{{\frac{3}{2}\pi }}^{{2\pi }}{{\frac{1}{2}\left( {{{\bf{e}}^9} - 1} \right)\,d\theta }}\end{align*}\] Show Step 5Finally, here is the really simple \(\theta \) integration.
\[\begin{align*}\int_{0}^{3}{{\int_{{ - \sqrt {9 - {x^{\,2}}} }}^{0}{{\,\,\,{{\bf{e}}^{{x^{\,2}} + {y^{\,2}}}}\,dy}}\,dx}} & = \int_{{\frac{3}{2}\pi }}^{{2\pi }}{{\frac{1}{2}\left( {{{\bf{e}}^9} - 1} \right)\,d\theta }}\\ & = \left. {\frac{1}{2}\left( {{{\bf{e}}^9} - 1} \right)\theta } \right|_{\frac{3}{2}\pi }^{2\pi } = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{1}{4}\pi \left( {{{\bf{e}}^9} - 1} \right) = 6363.3618}}\end{align*}\]