Section 15.4 : Double Integrals in Polar Coordinates
6. Use a double integral to determine the volume of the solid that is inside the cylinder \({x^2} + {y^2} = 16\), below \(z = 2{x^2} + 2{y^2}\) and above the \(xy\)-plane.
Show All Steps Hide All Steps
Start SolutionLet’s start off this problem with a quick sketch of the solid we’re looking at here in this problem.
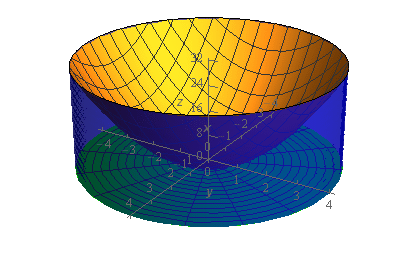
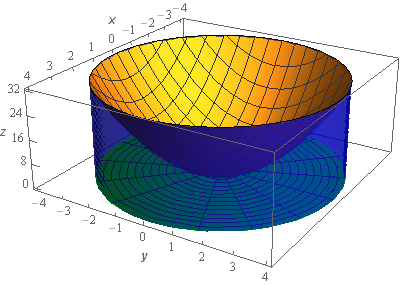
The top of the solid is the paraboloid (the gold colored surface in the sketches). The walls of the solid are the cylinder \({x^2} + {y^2} = 16\) and is shown with the semi translucent surface in the sketch. The bottom of the solid is the \(xy\)-plane.
Show Step 2So, the volume of the solid that is under the paraboloid and above the region \(D\) in the \(xy\)‑plane is given by,
\[V = \iint\limits_{D}{{2{x^2} + 2{y^2}\,dA}}\] Show Step 3The region \(D\) is the region from the \(xy\)-plane that we use to sketch the surface we are finding the volume under (i.e. the paraboloid).
Determining \(D\) in this case is pretty simple if you think about it. The solid is defined by the portion of the paraboloid that is inside the cylinder \({x^2} + {y^2} = 16\). But this is exactly what defines the portion of the \(xy\)-plane that we use to graph the surface. We only use the points from the \(xy\)-plane that are inside the cylinder and so the region \(D\) is then just the disk defined by \({x^2} + {y^2} \le 16\).
Another way to think of determining \(D\) for this case is to look at the solid from directly above it. The 2D region that you see will be the region \(D\). In this case the region we see is the inside of the cylinder or the disk \({x^2} + {y^2} \le 16\).
Now, the region \(D\) is a disk and so this strongly suggests that we use polar coordinates for this problem. The polar limits for this region \(D\) is,
\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le 4\end{array}\] Show Step 4Okay, let’s step up the integral in terms of polar coordinates.
\[V = \iint\limits_{D}{{2{x^2} + 2{y^2}\,dA}} = \int_{0}^{{2\pi }}{{\int_{0}^{4}{{\,\,\,\left( {2{r^2}} \right)\left( r \right)\,dr}}\,d\theta }} = \int_{0}^{{2\pi }}{{\int_{0}^{4}{{\,\,\,2{r^3}\,dr}}\,d\theta }}\]Don’t forget to convert all the \(x\)’s and \(y\)’s into \(r\)’s and \(\theta \)’s and make sure that you simplify the integrand as much as possible. Also, don’t forget to add in the \(r\) we get from the \(dA\).
Show Step 5Here is the simple \(r\) integration.
\[\begin{align*}V & = \int_{0}^{{2\pi }}{{\int_{0}^{4}{{\,\,\,2{r^3}\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\left. {\frac{1}{2}{r^4}} \right|_0^4\,d\theta }} = \int_{0}^{{2\pi }}{{128\,d\theta }}\end{align*}\] Show Step 6Finally, here is the really simple \(\theta \) integration.
\[V = \int_{0}^{{2\pi }}{{128\,d\theta }} = \require{bbox} \bbox[2pt,border:1px solid black]{{256\pi }}\]Note that this was a very simple integration and so we didn’t actually do any of the work and left it to you to verify the details.