Section 15.4 : Double Integrals in Polar Coordinates
7. Use a double integral to determine the volume of the solid that is bounded by \(z = 8 - {x^2} - {y^2}\) and \(z = 3{x^2} + 3{y^2} - 4\).
Show All Steps Hide All Steps
Start SolutionLet’s start off this problem with a quick sketch of the solid we’re looking at here in this problem.

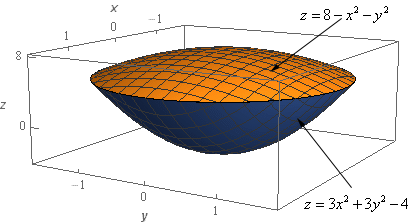
The top of the solid is the paraboloid given by \(z = 8 - {x^2} - {y^2}\) (the gold colored surface in the sketches) and the bottom of the solid is the paraboloid given by \(z = 3{x^2} + 3{y^2} - 4\) (the blue colored surface in the sketches).
Show Step 2To get the volume of this solid we’re going to need to know that value of \(z\) where these two surfaces intersect. To let’s solve the equation of the upper paraboloid as follow,
\[z = 8 - {x^2} - {y^2}\hspace{0.25in}\,\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}{x^2} + {y^2} = 8 - z\]Now plug this into the equation of the second paraboloid to get,
\[z = 3\left( {{x^2} + {y^2}} \right) - 4 = 3\left( {8 - z} \right) - 4 = 20 - 3z\hspace{0.25in} \to \hspace{0.25in}4z = 20 \hspace{0.25in} \to \hspace{0.25in} z = 5\]So, we know they will intersect at \(z = 5\). Plugging this into the either paraboloid equation and doing a little simplification will give the following equation.
\[{x^2} + {y^2} = 3\]Now, what does this tell us? This is the circle where the two paraboloids intersect at \(z = 5\). This is also tells us that the region \(D\) in the \(xy\)-plane that we are going to use in this problem is the disk defined by \({x^2} + {y^2} \le 3\). This makes sense if you think about it. It is the region in the \(xy\)-plane that we’d use to graph each of the paraboloids in the sketches.
Show Step 3We don’t have a formula to find the volume of this solid at this point so let’s see if we can figure out what it is.
Let’s start with the volume of just the lower portion of the solid. In other words, what is the volume of the portion of the solid that is below the plane \(z = 5\) and above the paraboloid given by \(z = 3{x^2} + 3{y^2} - 4\).
We looked at a solid like this in the notes for this section. Following the same logic in that problem the volume of the lower portion of the solid is given by,
\[{V_{{\mbox{lower}}}} = \iint\limits_{D}{{5 - \left( {3{x^2} + 3{y^2} - 4} \right)\,dA}} = \iint\limits_{D}{{9 - 3{x^2} - 3{y^2}\,dA}}\]where \(D\) is the disk \({x^2} + {y^2} \le 3\) as we discussed above.
Note that even though this paraboloid does slip under the \(xy\)-plane the formula is still valid.
Show Step 4The volume of the upper portion of the solid, i.e. the portion under \(z = 8 - {x^2} - {y^2}\) and above the plane \(z = 5\) can be found with a similar argument to the one we used for the lower region. The volume of the upper region is then,
\[{V_{{\mbox{upper}}}} = \iint\limits_{D}{{8 - {x^2} - {y^2} - \left( 5 \right)\,dA}} = \iint\limits_{D}{{3 - {x^2} - {y^2}\,dA}}\]where \(D\) is the disk \({x^2} + {y^2} \le 3\) as we discussed above.
The volume of the whole solid is then,
\[\begin{align*}V & = {V_{{\mbox{lower}}}} + {V_{{\mbox{upper}}}}\\ & = \iint\limits_{D}{{9 - 3{x^2} - 3{y^2}\,dA}} + \iint\limits_{D}{{3 - {x^2} - {y^2}\,dA}}\\ & = \iint\limits_{D}{{9 - 3{x^2} - 3{y^2} + \left( {3 - {x^2} - {y^2}} \right)\,dA}}\\ & = \iint\limits_{D}{{12 - 4{x^2} - 4{y^2}\,dA}}\end{align*}\]Note that we could combine the two integrals because they were both over the same region \(D\).
Show Step 5Okay, as we’ve already determined \(D\) is the disk given by \({x^2} + {y^2} \le 3\) and because this is a disk it makes sense to do this integral in polar coordinates. Here are the polar limits for this integral/region.
\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le \sqrt 3 \end{array}\] Show Step 6The volume integral (in terms of polar coordinates) is then,
\[\begin{align*}V & = \iint\limits_{D}{{12 - 4{x^2} - 4{y^2}\,dA}}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{{\sqrt 3 }}{{\left( {12 - 4{r^2}} \right)\left( r \right)\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{{\sqrt 3 }}{{12r - 4{r^3}\,dr}}\,d\theta }}\end{align*}\]Don’t forget to convert all the \(x\)’s and \(y\)’s into \(r\)’s and \(\theta \)’s and make sure that you simplify the integrand as much as possible. Also, don’t forget to add in the \(r\) we get from the \(dA\).
Show Step 7Here is the \(r\) integration.
\[\begin{align*}V &= \int_{0}^{{2\pi }}{{\int_{0}^{{\sqrt 3 }}{{12r - 4{r^3}\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\left. {\left( {6{r^2} - {r^4}} \right)} \right|_0^{\sqrt 3 }\,d\theta }} = \int_{0}^{{2\pi }}{{9\,d\theta }}\end{align*}\] Show Step 8Finally, here is the really simple \(\theta \) integration.
\[V = \int_{0}^{{2\pi }}{{9\,d\theta }} = \require{bbox} \bbox[2pt,border:1px solid black]{{18\pi }}\]Note that this was a very simple integration and so we didn’t actually do any of the work and left it to you to verify the details.