Section 17.6 : Divergence Theorem
1. Use the Divergence Theorem to evaluate \( \displaystyle \iint\limits_{S}{{\vec F\centerdot d\vec S}}\) where \(\vec F = y{x^2}\,\vec i + \left( {x{y^2} - 3{z^4}} \right)\,\vec j + \left( {{x^3} + {y^2}} \right)\,\vec k\) and \(S\) is the surface of the sphere of radius 4 with \(z \le 0\) and \(y \le 0\). Note that all three surfaces of this solid are included in \(S\).
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.

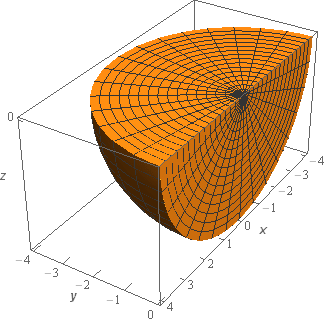
We included a sketch with traditional axes and a sketch with a set of “box” axes to help visualize the surface.
Note as well here that because we are including all three surfaces shown above that the surface does enclose (or is the boundary curve if you want to use that terminology) the portion of the sphere shown above.
Show Step 2We are going to use the Divergence Theorem in the following direction.
\[\iint\limits_{S}{{\vec F\centerdot d\vec S}} = \iiint\limits_{E}{{{\mathop{\rm div}\nolimits} \vec F\,dV}}\]where \(E\) is just the solid shown in the sketches from Step 1.
Because \(E\) is a portion of a sphere we’ll be wanting to use spherical coordinates for the integration. Here are the spherical limits we’ll need to use for this region.
\[\begin{array}{c}\pi \le \theta \le 2\pi \\ \displaystyle \frac{\pi }{2} \le \varphi \le \pi \\ 0 \le \rho \le 4\end{array}\]One of the restrictions on the region in the problem statement was \(y \le 0\). This means that if we look at this from above we’d see the portion of the circle of radius 4 that is below the \(x\) axis and so we need the given range of \(\theta \) above to cover this region.
We were also told in the problem statement that \(z \le 0\) and so we only want the portion of the sphere that is below the \(xy\)-plane. We therefore need the given range of \(\varphi \) to make sure we are only below the \(xy\)-plane.
We’ll also need the divergence of the vector field so here is that.
\[{\mathop{\rm div}\nolimits} \vec F = \frac{\partial }{{\partial x}}\left( {y{x^2}} \right) + \frac{\partial }{{\partial y}}\left( {x{y^2} - 3{z^4}} \right) + \frac{\partial }{{\partial z}}\left( {{x^3} + {y^2}} \right) = 4xy\] Show Step 3Now let’s apply the Divergence Theorem to the integral and get it converted to spherical coordinates while we’re at it.
\[\begin{align*}\iint\limits_{S}{{\vec F\centerdot d\vec S}} & = \iiint\limits_{E}{{{\mathop{\rm div}\nolimits} \vec F\,dV}}\\ & = \iiint\limits_{E}{{4xy\,dV}}\\ & = \int_{\pi }^{{2\pi }}{{\int_{{\frac{1}{2}\pi }}^{\pi }{{\int_{0}^{4}{{4\left( {\rho \sin \varphi \cos \theta } \right)\left( {\rho \sin \varphi \sin \theta } \right)\left( {{\rho ^2}\sin \varphi } \right)\,d\rho }}\,d\varphi }}\,d\theta }}\\ & = \int_{\pi }^{{2\pi }}{{\int_{{\frac{1}{2}\pi }}^{\pi }{{\int_{0}^{4}{{4{\rho ^4}{{\sin }^3}\varphi \cos \theta \sin \theta \,d\rho }}\,d\varphi }}\,d\theta }}\end{align*}\]Don’t forget to pick up the \({\rho ^2}\sin \varphi \) when converting the \(dV\) to spherical coordinates.
Show Step 4All we need to do then in evaluate the integral.
\[\begin{align*}\iint\limits_{S}{{\vec F\centerdot d\vec S}} & = \int_{\pi }^{{2\pi }}{{\int_{{\frac{1}{2}\pi }}^{\pi }{{\int_{0}^{4}{{4{\rho ^4}{{\sin }^3}\varphi \cos \theta \sin \theta \,d\rho }}\,d\varphi }}\,d\theta }}\\ & = \int_{\pi }^{{2\pi }}{{\int_{{\frac{1}{2}\pi }}^{\pi }{{\left. {\left( {\frac{4}{5}{\rho ^5}{{\sin }^3}\varphi \cos \theta \sin \theta } \right)} \right|_0^4\,d\varphi }}\,d\theta }}\\ & = \int_{\pi }^{{2\pi }}{{\int_{{\frac{1}{2}\pi }}^{\pi }{{\frac{{4096}}{5}\sin \varphi \left( {1 - {{\cos }^2}\varphi } \right)\cos \theta \sin \theta \,d\varphi }}\,d\theta }}\\ & = \int_{\pi }^{{2\pi }}{{\left. {\left( { - \frac{{4096}}{5}\left( {\cos \varphi - \frac{1}{3}{{\cos }^3}\varphi } \right)\cos \theta \sin \theta } \right)} \right|_{\frac{1}{2}\pi }^\pi \,d\theta }}\\ & = \int_{\pi }^{{2\pi }}{{\frac{{8192}}{{15}}\cos \theta \sin \theta \,d\theta }}\\ & = \int_{\pi }^{{2\pi }}{{\frac{{4096}}{{15}}\sin \left( {2\theta } \right)\,d\theta }}\\ & = \left. {-\frac{{2048}}{{15}}\cos \left( {2\theta } \right)} \right|_\pi ^{2\pi } = \require{bbox} \bbox[2pt,border:1px solid black]{0}\end{align*}\]Make sure you can do use your trig formulas as we did here to deal with these kinds of integrals!