Section 17.4 : Surface Integrals of Vector Fields
4. Evaluate \( \displaystyle \iint\limits_{S}{{\vec F\centerdot \,d\vec S}}\) where \(\vec F = \,\vec i + z\,\vec j + 6x\,\vec k\) and \(S\) is the portion of the sphere of radius 3 with \(x \le 0\), \(y \ge 0\) and \(z \ge 0\) oriented inward (i.e. towards the origin).
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.
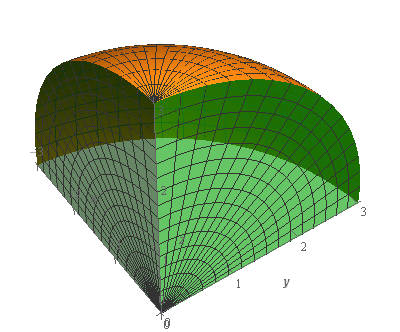
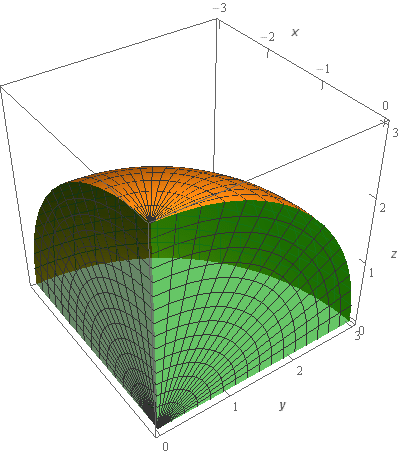
Note that the surface in this problem is only the part of the sphere itself. The “edges” (the greenish portions on the right/left) are not part of this surface despite the fact that they are in the sketch. They were included in the sketch to try and make the surface a little clearer in the sketch. We would only include the “edges” if the problem had specified that in some manner to make it clear.
Show Step 2Let’s get the integral set up now. In this case the we are integrating over a sphere and so we’ll need to set up a parameterization for the surface.
We saw how to parameterize a sphere in the first section of this chapter so we won’t go into detail for the parameterization. The parameterization is,
\[\vec r\left( {\theta ,\varphi } \right) = \left\langle {3\sin \varphi \cos \theta ,3\sin \varphi \sin \theta ,3\cos \varphi } \right\rangle \hspace{0.25in}\,\,\,\,\frac{1}{2}\pi \le \theta \le \pi ,\,\,\,\,\,0 \le \varphi \le \frac{1}{2}\pi \]We needed the restriction on \(\varphi \) to make sure that we only get a portion of the upper half of the sphere (i.e.\(z \ge 0\)). Likewise the restriction on \(\theta \) was needed to get only the portion that was in the 2nd quadrant of the \(xy\)-plane (i.e. \(x \le 0\) and \(y \ge 0\)).
Next, we’ll need to compute the cross product.
\[{\vec r_\theta } = \left\langle { - 3\sin \varphi \sin \theta ,3\sin \varphi \cos \theta ,0} \right\rangle \hspace{0.25in}\hspace{0.25in}{\vec r_\varphi } = \left\langle {3\cos \varphi \cos \theta ,3\cos \varphi \sin \theta , - 3\sin \varphi } \right\rangle \] \[\begin{align*}{{\vec r}_\theta } \times {{\vec r}_\varphi } & = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\{ - 3\sin \varphi \sin \theta }&{3\sin \varphi \cos \theta }&0\\{3\cos \varphi \cos \theta }&{3\cos \varphi \sin \theta }&{ - 3\sin \varphi }\end{array}} \right|\\ & = - 9{\sin ^2}\varphi \cos \theta \,\vec i - 9\sin \varphi \cos \varphi {\sin ^2}\theta \vec k - 9\sin \varphi \cos \varphi {\cos ^2}\theta \vec k - 9{\sin ^2}\varphi \sin \theta \vec j\\ & = - 9{\sin ^2}\varphi \cos \theta \,\vec i - 9{\sin ^2}\varphi \sin \theta \vec j - 9\sin \varphi \cos \varphi \left( {{{\sin }^2}\theta + {{\cos }^2}\theta } \right)\vec k\\ & = - 9{\sin ^2}\varphi \cos \theta \,\vec i - 9{\sin ^2}\varphi \sin \theta \vec j - 9\sin \varphi \cos \varphi \vec k\end{align*}\]A unit normal vector for the surface is then,
\[\vec n = \frac{{{{\vec r}_\theta } \times {{\vec r}_\varphi }}}{{\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|}} = \frac{{\left\langle { - 9{{\sin }^2}\varphi \cos \theta , - 9{{\sin }^2}\varphi \sin \theta , - 9\sin \varphi \cos \varphi } \right\rangle }}{{\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|}}\]We didn’t compute the magnitude of the cross product since we know that it will just cancel out when we start working with the integral.
Now we need to determine if this vector has the correct orientation. We know that the normal vector needs to point in towards the origin. Let’s think about what that would mean for a normal vector on the upper half of a sphere and it won’t matter which quadrant in the \(xy\)-plane we are in.
If we are on the upper half of a sphere and the normal vectors must point towards the origin then we know that they will all need to point downwards. They could point in the positive or negative \(x\) (or \(y\)) direction depending on which quadrant from the \(xy\)-plane we are on but they will have to all point downwards. Or in other words, the \(z\) component must be negative.
So, the \(z\) component of the normal vector above is \( - 9\sin \varphi \cos \varphi \) and we know that we are restricted to \(0 \le \varphi \le \frac{1}{2}\pi \) for the portion of the sphere we are working on in this problem. In this range of \(\varphi \) we know that both sine and cosine are positive and so the \(z\) component must always be negative. This means that the normal vector above has the correct orientation for this problem.
Note that if we were on the lower half of a sphere (not relevant for this problem but useful to think about anyway) and the normal vector would be pointing towards the origin and so they would have to all be pointing upwards.
Also note that if the normal vectors were all pointing out away from the origin then we’d just need to multiply the normal vector above by minus one to get the normal vector we’d need.
Show Step 3Next, we’ll need to compute the following dot product.
\[\begin{align*}\vec F\left( {\vec r\left( {\theta ,\varphi } \right)} \right)\centerdot \vec n & = \left\langle {1,3\cos \varphi ,18\sin \varphi \cos \theta } \right\rangle \centerdot \frac{{\left\langle { - 9{{\sin }^2}\varphi \cos \theta , - 9{{\sin }^2}\varphi \sin \theta , - 9\sin \varphi \cos \varphi } \right\rangle }}{{\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|}}\\ & = \frac{1}{{\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|}}\left( { - 9{{\sin }^2}\varphi \cos \theta - 27{{\sin }^2}\varphi \cos \varphi \sin \theta - 162{{\sin }^2}\varphi \cos \varphi \cos \theta } \right)\\ & = \frac{1}{{\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|}}\left( { - \frac{9}{2}\left( {1 - \cos \left( {2\varphi } \right)} \right)\cos \theta - {{\sin }^2}\varphi \cos \varphi \left( {27\sin \theta + 162\cos \theta } \right)} \right)\end{align*}\]Note that we did a little simplification for the integration process in the last step above.
The integral is then,
\[\begin{align*}\iint\limits_{S}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{S}{{\frac{1}{{\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|}}\left( { - \frac{9}{2}\left( {1 - \cos \left( {2\varphi } \right)} \right)\cos \theta - {{\sin }^2}\varphi \cos \varphi \left( {27\sin \theta + 162\cos \theta } \right)} \right)\,dS}}\\ & = \iint\limits_{D}{{\frac{1}{{\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|}}\left( { - \frac{9}{2}\left( {1 - \cos \left( {2\varphi } \right)} \right)\cos \theta - {{\sin }^2}\varphi \cos \varphi \left( {27\sin \theta + 162\cos \theta } \right)} \right)\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|\,dA}}\\ & = \iint\limits_{D}{{ - \frac{9}{2}\left( {1 - \cos \left( {2\varphi } \right)} \right)\cos \theta - {{\sin }^2}\varphi \cos \varphi \left( {27\sin \theta + 162\cos \theta } \right)\,dA}}\end{align*}\]As noted above we didn’t need to compute the magnitude of the cross product since it would just cancel out when we converted the surface integral into a “normal” double integral.
Also, recall that \(D\) is given by the limits on \(\theta \) and \(\varphi \) we found at the start of Step 2.
Show Step 4Now all that we need to do is evaluate the double integral and that shouldn’t be too difficult at this point.
The integral is then,
\[\begin{align*}\iint\limits_{S}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{D}{{ - \frac{9}{2}\left( {1 - \cos \left( {2\varphi } \right)} \right)\cos \theta - {{\sin }^2}\varphi \cos \varphi \left( {27\sin \theta + 162\cos \theta } \right)\,dA}}\\ & = \int_{{\frac{1}{2}\pi }}^{\pi }{{\int_{0}^{{\frac{1}{2}\pi }}{{ - \frac{9}{2}\left( {1 - \cos \left( {2\varphi } \right)} \right)\cos \theta - {{\sin }^2}\varphi \cos \varphi \left( {27\sin \theta + 162\cos \theta } \right)\,d\varphi }}\,d\theta }}\\ & = \int_{{\frac{1}{2}\pi }}^{\pi }{{\left. { - \frac{9}{2}\left( {\varphi - \frac{1}{2}\sin \left( {2\varphi } \right)} \right)\cos \theta - \frac{1}{3}{{\sin }^3}\varphi \left( {27\sin \theta + 162\cos \theta } \right)} \right|_0^{\frac{1}{2}\pi }\,d\theta }}\\ & = \int_{{\frac{1}{2}\pi }}^{\pi }{{ - \frac{9}{4}\pi \cos \theta - 9\sin \theta - 54\cos \theta \,d\theta }}\\ & = \left. {\left( { - \frac{9}{4}\pi \sin \theta + 9\cos \theta - 54\sin \theta } \right)} \right|_{\frac{1}{2}\pi }^\pi = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{9}{4}\pi + 45}}\end{align*}\]