Section 17.4 : Surface Integrals of Vector Fields
5. Evaluate \( \displaystyle \iint\limits_{S}{{\vec F\centerdot \,d\vec S}}\) where \(\vec F = y\,\vec i + 2x\,\vec j + \left( {z - 8} \right)\,\vec k\) and \(S\) is the surface of the solid bounded by \(4x + 2y + z = 8\), \(z = 0\), \(y = 0\) and \(x = 0\) with the positive orientation. Note that all four surfaces of this solid are included in \(S\).
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.
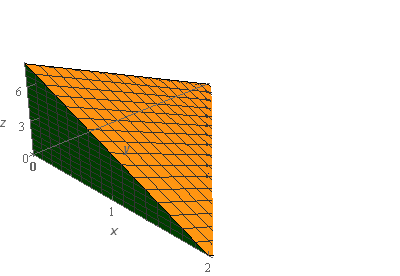
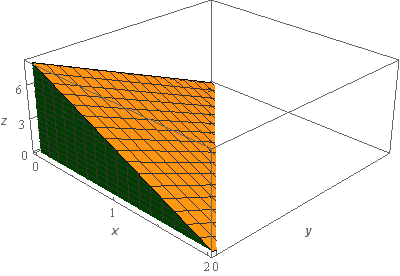
Okay, as noted in the problem statement all four surfaces in the sketch (two not shown) are part of \(S\) so let’s define each of them as follows.
\({S_1}:{\mbox{ Plane given by }}4x + 2y + z = 8{\mbox{ }}\left( {i.e{\mbox{ the top of the solid}}} \right)\)
\({S_2}:{\mbox{ Plane given by }}y = 0{\mbox{ }}\left( {i.e{\mbox{ the triangle on right side of the solid}}} \right)\)
\({S_3}:{\mbox{ Plane given by }}x = 0{\mbox{ }}\left( {i.e{\mbox{ the triangle at back of the solid - not shown in sketch}}} \right)\)
\({S_4}:{\mbox{ Plane given by }}z = 0{\mbox{ }}\left( {i.e{\mbox{ the triangle on bottom of the solid - not shown in sketch}}} \right)\)
As noted in the definitions above the first two surfaces are shown in the sketch but the last two are not actually shown due to the orientation of the solid. Below are sketches of each of the three surfaces that correspond to the coordinates planes.
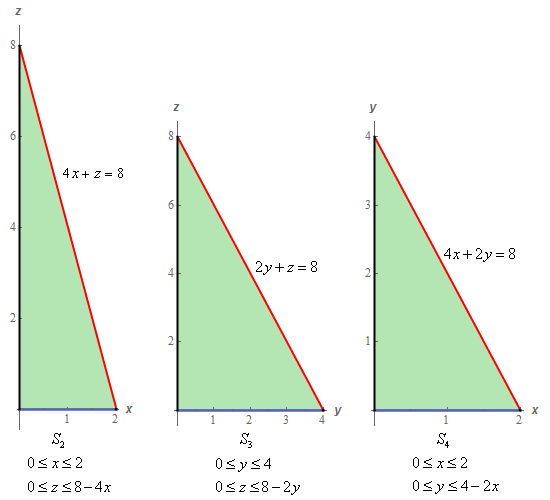
With each of the sketches we gave limits on the variables for each of them since we’ll eventually need that when we start doing the surface integral along each surface.
Now we need to go through and do the integral for each of these surfaces and we’re going to go through these a little quicker than we did for the first few problems in this section.
Show Step 2Let’s start with \({S_1}\). In this case we can write the equation of the plane as follows,
\[f\left( {x,y,z} \right) = 4x + 2y + z - 8 = 0\]A unit normal vector for the surface is then,
\[\vec n = \frac{{\nabla f}}{{\left\| {\nabla f} \right\|}} = \frac{{\left\langle {4,2,1} \right\rangle }}{{\left\| {\nabla f} \right\|}}\]We didn’t compute the magnitude of the gradient since we know that it will just cancel out when we start working with the integral.
The surface has the positive orientation and so must point outwards from the region enclosed by the surface. This means that normal vectors on this plane will need to be pointing generally upwards (i.e. have a positive \(z\) component) which this normal vector does.
Now we’ll need the following dot product and don’t forget to plug in the equation of the plane (solved for \(z\) of course) into \(z\) in the vector field.
\[\begin{align*}\vec F\left( {x,y,8 - 4x - 2y} \right)\centerdot \vec n & = \left\langle {y,2x, - 4x - 2y} \right\rangle \centerdot \frac{{\left\langle {4,2,1} \right\rangle }}{{\left\| {\nabla f} \right\|}}\\ & = \frac{1}{{\left\| {\nabla f} \right\|}}\left( {2y} \right)\end{align*}\]The integral is then,
\[\begin{align*}\iint\limits_{{{S_1}}}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{{{S_1}}}{{\frac{1}{{\left\| {\nabla f} \right\|}}\left( {2y} \right)\,dS}}\\ & = \iint\limits_{D}{{\frac{1}{{\left\| {\nabla f} \right\|}}\left( {2y} \right)\left\| {\nabla f} \right\|\,dA}}\\ & = \iint\limits_{D}{{2y\,dA}}\end{align*}\]In this case \(D\) is just \({S_4}\) and so we can now finish out the integral.
\[\begin{align*}\iint\limits_{{{S_1}}}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{D}{{2y\,dA}}\\ & = \int_{0}^{2}{{\int_{0}^{{4 - 2x}}{{2y\,dy}}\,dx}}\\ & = \int_{0}^{2}{{\left. {{y^2}} \right|_0^{4 - 2x}\,dx}}\\ & = \int_{0}^{2}{{{{\left( {4 - 2x} \right)}^2}\,dx}}\\ & = \left. { - \frac{1}{6}{{\left( {4 - 2x} \right)}^3}} \right|_0^2 = \underline {\frac{{32}}{3}} \end{align*}\] Show Step 3Next, we’ll take care of \({S_2}\). In this case the equation for the surface is simply \(y = 0\) and \(D\) is given in the sketch of \({S_2}\) in Step 1.
In this case \({S_2}\) is simply a portion of the \(xz\)-plane and we have the positive orientation and so the normal vector must point away from the region enclosed by the surface. That means that, in this case, the normal vector is simply \(\vec n = - \vec j = \left\langle {0, - 1,0} \right\rangle \).
The dot product for this surface is,
\[\vec F\left( {x,0,z} \right)\centerdot \vec n = \left\langle {0,2x,z - 8} \right\rangle \centerdot \frac{{\left\langle {0, - 1,0} \right\rangle }}{1} = - 2x\]Don’t forget to plug \(y = 0\) into the vector field and note that the magnitude of the gradient is,
\[\left\| {\nabla f} \right\| = \sqrt {{{\left( 0 \right)}^2} + {{\left( 1 \right)}^2} + {{\left( 0 \right)}^2}} = 1\]The integral is then,
\[\begin{align*}\iint\limits_{{{S_2}}}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{{{S_2}}}{{ - 2x\,dS}}\\ & = \iint\limits_{D}{{ - 2x\left( 1 \right)\,dA}}\\ & = \int_{0}^{2}{{\int_{0}^{{8 - 4x}}{{ - 2x\,dz}}\,dx}}\\ & = \int_{0}^{2}{{\left. { - 2xz} \right|_0^{8 - 4x}\,dx}}\\ & = \int_{0}^{2}{{8{x^2} - 16x\,dx}}\\ & = \left. {\left( {\frac{8}{3}{x^3} - 8{x^2}} \right)} \right|_0^2 = \underline { - \frac{{32}}{3}} \end{align*}\] Show Step 4Now we can deal with \({S_3}\). In this case the equation for the surface is simply \(x = 0\) and \(D\) is given in the sketch of \({S_3}\) in Step 1.
In this case \({S_3}\) is simply a portion of the \(yz\)-plane and we have the positive orientation and so the normal vector must point away from the region enclosed by the surface. That means that, in this case, the normal vector is simply \(\vec n = - \vec i = \left\langle { - 1,0,0} \right\rangle \).
The dot product for this surface is,
\[\vec F\left( {0,y,z} \right)\centerdot \vec n = \left\langle {y,0,z - 8} \right\rangle \centerdot \frac{{\left\langle { - 1,0,0} \right\rangle }}{1} = - y\]Don’t forget to plug \(x = 0\) into the vector field and note that the magnitude of the gradient is,
\[\left\| {\nabla f} \right\| = \sqrt {{{\left( 1 \right)}^2} + {{\left( 0 \right)}^2} + {{\left( 0 \right)}^2}} = 1\]The integral is then,
\[\begin{align*}\iint\limits_{{{S_3}}}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{{{S_3}}}{{ - y\,dS}}\\ & = \iint\limits_{D}{{ - y\left( 1 \right)\,dA}}\\ & = \int_{0}^{4}{{\int_{0}^{{8 - 2y}}{{ - y\,dz}}\,dy}}\\ & = \int_{0}^{4}{{\left. { - yz} \right|_0^{8 - 2y}\,dy}}\\ & = \int_{0}^{4}{{2{y^2} - 8y\,dy}}\\ & = \left. {\left( {\frac{2}{3}{y^3} - 4{y^2}} \right)} \right|_0^4 = \underline { - \frac{{64}}{3}} \end{align*}\] Show Step 5Finally let’s take care of \({S_4}\). In this case the equation for the surface is simply \(z = 0\) and \(D\) is given in the sketch of \({S_4}\) in Step 1.
In this case \({S_4}\) is simply a portion of the \(xy\)-plane and we have the positive orientation and so the normal vector must point away from the region enclosed by the surface. That means that, in this case, the normal vector is simply \(\vec n = - \vec k = \left\langle {0,0, - 1} \right\rangle \).
The dot product for this surface is,
\[\vec F\left( {x,y,0} \right)\centerdot \vec n = \left\langle {y,2x, - 8} \right\rangle \centerdot \frac{{\left\langle {0,0, - 1} \right\rangle }}{1} = 8\]Don’t forget to plug \(z = 0\) into the vector field and note that the magnitude of the gradient is,
\[\left\| {\nabla f} \right\| = \sqrt {{{\left( 0 \right)}^2} + {{\left( 0 \right)}^2} + {{\left( 1 \right)}^2}} = 1\]The integral is then,
\[\begin{align*}\iint\limits_{{{S_4}}}{{\vec F\centerdot \,d\vec S}} & = \iint\limits_{{{S_4}}}{{8\,dS}}\\ & = \iint\limits_{D}{{8\,dA}}\\ & = 8\iint\limits_{D}{{dA}}\\ & = 8\left( {{\mbox{Area of }}D} \right)\\ & = 8\left( {\frac{1}{2}} \right)\left( 2 \right)\left( 4 \right) = \underline {32} \end{align*}\]In this case notice that we didn’t have to actually compute the double integral since \(D\) was just a right triangle and we can easily compute its area.
Show Step 6Now, to get the value of the integral over the full surface all we need to do is sum up the values of each of the integrals over the four surfaces above. Doing this gives,
\[\iint\limits_{S}{{\vec F\centerdot \,d\vec S}} = \left( {\frac{{32}}{3}} \right) + \left( { - \frac{{32}}{3}} \right) + \left( { - \frac{{64}}{3}} \right) + \left( {32} \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{32}}{3}}}\]We put parenthesis around each of the individual integral values just to indicate where each came from. In general, these aren’t needed of course.