Section 15.5 : Triple Integrals
6. Evaluate \( \displaystyle \iiint\limits_{E}{{yz\,dV}}\) where \(E\) is the region bounded by \(x = 2{y^2} + 2{z^2} - 5\) and the plane \(x = 1\).
Show All Steps Hide All Steps
Start SolutionOkay, let’s start off with a quick sketch of the region \(E\) so we can get a feel for what we’re dealing with.
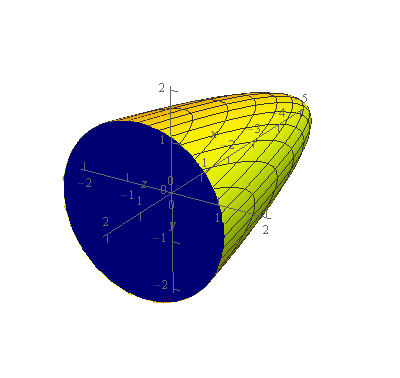
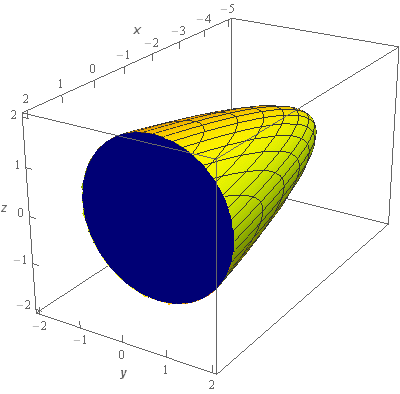
We’ve given the sketches with a set of “traditional” axes as well as a set of “box” axes to help visualize the surface and region.
We know that \(x = 2{y^2} + 2{z^2} - 5\) is an elliptic paraboloid that is centered on the \(x\)-axis and opens in the positive \(x\) direction as shown in the sketch above. The blue “cap” on the surface is the portion of the plane \(x = 1\) that fits just inside the paraboloid.
Show Step 2Okay, for this problem it is hopefully clear that we’ll need to integrate with respect to \(x\) first and that the region \(D\) will be in the y\(z\)-plane.
Therefore, we have the following limits for \(x\).
\[2{y^2} + 2{z^2} - 5 \le x \le 1\]Remember that when setting these kinds of limits up we go from back to front and so the paraboloid will be the lower limit since it is the surface that is in the “back” of the solid while \(x = 1\) is the “front” of the solid and so is the upper limit.
With these limits we can also get the triple integral at least partially set up as follows.
\[\iiint\limits_{E}{{yz\,dV}} = \iint\limits_{D}{{\left[ {\int_{{2{y^2} + 2{z^2} - 5}}^{1}{{yz\,dx}}} \right]\,dA}}\] Show Step 3Next, we’ll need limits for \(D\) so we can finish setting up the integral. To determine \(D\) we’ll need the intersection of the two surfaces. The intersection is,
\[2{y^2} + 2{z^2} - 5 = 1\hspace{0.25in} \to \hspace{0.25in} 2{y^2} + 2{z^2} = 6\hspace{0.25in} \to \hspace{0.25in}{y^2} + {z^2} = 3\]Now, if we looked at the solid from the “front”, i.e. from along the positive \(x\)-axis we’d see the disk \({y^2} + {z^2} \le 3\) and so this is the region \(D\).
The region \(D\) is a disk which clearly suggests polar coordinates, however, it won’t be the “standard” \(xy\) polar coordinates. Since \(D\) is in the \(yz\)-plane let’s use the following “modified” polar coordinates.
\[y = r\sin \theta \,\hspace{0.25in}z = r\cos \theta \hspace{0.25in}\hspace{0.25in}{y^2} + {z^2} = {r^2}\]This “definition” of polar coordinates for our problem isn’t needed quite yet but will be eventually.
At this point all we need are the polar limits for this circle and those should fairly clearly be given by,
\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le \sqrt 3 \end{array}\]With all the previous problems we’d write the integral down with these limits at this point as well. However, since we are going to have to convert to polar coordinates we’ll hold off writing down the integral in polar coordinates until we do the first integration.
Show Step 4So, here is the \(x\) integration.
\[\begin{align*}\iiint\limits_{E}{{yz\,dV}} & = \iint\limits_{D}{{\left. {\left( {xyz} \right)} \right|_{2{y^2} + 2{z^2} - 5}^1\,dA}}\\ & = \iint\limits_{D}{{\left[ {1 - \left( {2{y^2} + 2{z^2} - 5} \right)} \right]yz\,dA}}\\ & = \iint\limits_{D}{{\left[ {6 - 2\left( {{y^2} + {z^2}} \right)} \right]yz\,dA}}\end{align*}\]We did a small amount of simplification here in preparation for the next step.
Show Step 5Now we need to convert the integral over to polar coordinates using the modified version we defined in Step 3.
Here is the integral when converted to polar coordinates.
\[\begin{align*}\iiint\limits_{E}{{yz\,dV}} & = \int_{0}^{{2\pi }}{{\int_{0}^{{\sqrt 3 }}{{\left[ {6 - 2{r^2}} \right]\left( {r\sin \theta } \right)\left( {r\cos \theta } \right)r\,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\int_{0}^{{\sqrt 3 }}{{\left[ {6{r^3} - 2{r^5}} \right]\sin \theta \cos \theta \,dr}}\,d\theta }}\end{align*}\] Show Step 6Now let’s do the \(r\) integration.
\[\begin{align*}\iiint\limits_{E}{{yz\,dV}} & = \int_{0}^{{2\pi }}{{\left. {\left[ {\frac{3}{2}{r^4} - \frac{1}{3}{r^6}} \right]\sin \theta \cos \theta } \right|_0^{\sqrt 3 }\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\frac{9}{2}\sin \theta \cos \theta \,d\theta }}\end{align*}\] Show Step 7Finally, let’s do the \(\theta \) integration and notice that we’re going to use the double angle formula for sine to “simplify” the integral slightly prior to the integration.
\[\iiint\limits_{E}{{yz\,dV}} = \int_{0}^{{2\pi }}{{\frac{9}{4}\sin \left( {2\theta } \right)\,d\theta }} = \left. {\left( { - \frac{9}{8}\cos \left( {2\theta } \right)} \right)} \right|_0^{2\pi } = \require{bbox} \bbox[2pt,border:1px solid black]{0}\]So, once we got the limits all set up, the integration for this problem wasn’t too bad. That will often be the case with these problems. Getting the limits for the integrals set up will often, but not always, be the hardest part of the problem. Once they get set up the integration is often pretty simple.
Also, as we saw in this example it is not unusual for polar coordinates to show in the “outer” double integral and there is no reason to expect they will always be the “standard” \(xy\) definition of polar coordinates and so you will need to be ready to use them in any of the three orientations (\(xy\), \(xz\) or \(yz\)) in which they may show up.