Section 15.5 : Triple Integrals
7. Evaluate \( \displaystyle \iiint\limits_{E}{{15z\,dV}}\) where \(E\) is the region between \(2x + y + z = 4\) and \(4x + 4y + 2z = 20\) that is in front of the region in the \(yz\)-plane bounded by \(z = 2{y^2}\) and \(z = \sqrt {4y} \).
Show All Steps Hide All Steps
Start SolutionThis region always seems pretty difficult to visualize. So, let’s start off with the following sketch.
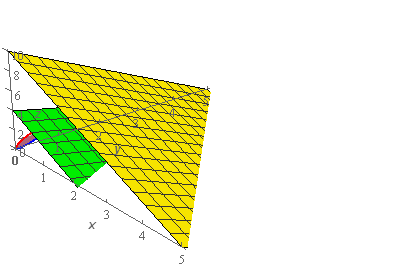
Note that the “orientation” of the \(x\) and \(y\) axes are different in this sketch form all the other 3D sketches we’ve done to this point. This is done to help with the visualization. Without the reorientation it would be very difficult to visualize the bounded region.
Do not always expect that the orientation of the axes to always remain fixed and never changing. Sometimes the orientation will need to change so we can visualize a particular surface or region.
Okay, onto the trying to visualize the region we are working with here.
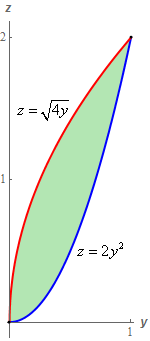
The yellow plane is the graph of \(4x + 4y + 2z = 20\) in the 1st octant (the only portion we’ll need here) and the green plane is the graph of \(2x + y + z = 4\). At the origin (kind of hard to see) is the sketch of the bounded region in the \(yz\)-plane referenced in the problem statement. Because this bounded region is hard to see on the graph above here is separate graph of just the bounded region.
Now, to try and visualize the region \(E\), imagine that there is a lump of cookie dough between the two planes in the first sketch above and the bounded region in the \(yz\)-plane is a cookie cutter. We move the bounded region away from the \(yz\)-plane making sure to always keep it parallel to the \(yz\)-plane.
As the bounded region moves out the top of it will first cut into the “cookie dough” when it hits the green plane and will be fully in the cookie dough when the bottom of the bounded region hits the green plane. The bounded region will continue to cut through the cookie dough until it reaches the yellow plane with the top of the bounded region exiting the cookie dough first when it hits the yellow plane. The bounded region will be fully out of the cookie dough when the bottom of the bounded region hits the yellow plane.
Here is a sketch of the path that the bounded region takes as it moves away from the \(yz\)‑plane.
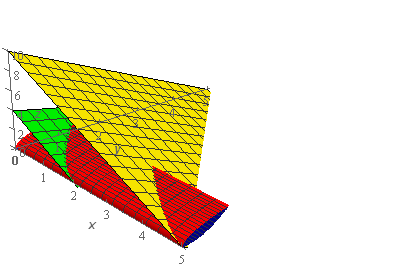
Note that this sketch shows the full path of the bounded region regardless of whether or not it is between the two planes. Or using the analogy from above regardless of whether or not it is cutting out a region from the cookie dough between the two planes. The region \(E\) that we are after is just the portion of this path that lies between the two planes.
Here is a sketch of the path of the bounded region that is only between the two planes.
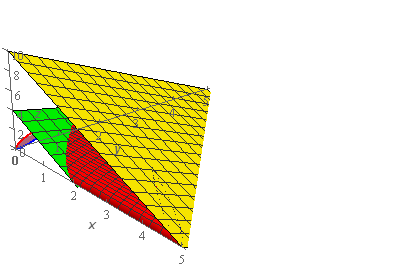
The top of the region \(E\) is the red portion shown above. It is kind of hard however to visualize the full region with the two planes still in the sketch. So, here is another sketch with two planes removed from the sketch.
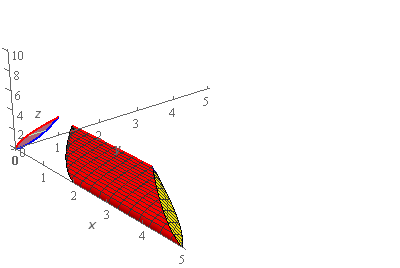
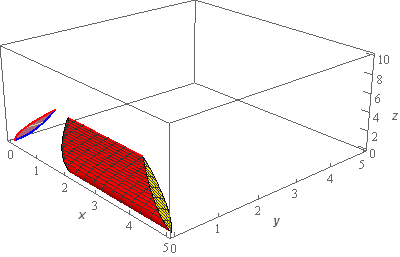
The region \(E\) is then the solid shown above. The “front” of \(E\) is sloped and follows the yellow plane (and hence is also shaded yellow to make this clearer) and the “rear” of \(E\) is sloped and follows the green plane.
With this final sketch of the region \(E\) we included both the “traditional” axis system as well as the “boxed” axes system to help visualize the object. We also kept the same \(x\), \(y\), \(z\) scale as the previous images to helpful help with the visualization even though there is a lot of “wasted” space in the right side of the axes system.
Show Step 2Okay, for this problem the problem statement tells us that the bounded region, i.e. \(D\), is in the \(yz\)-plane and we we’ll need to integrate with respect to \(x\) first.
This means we’ll need to solve each of the equations of the planes for \(x\) and we’ll integrate from the back (or green) plane up to the front (or yellow) plane.
Therefore, we have the following limits for \(x\).
\[2 - \frac{1}{2}y - \frac{1}{2}z \le x \le 5 - y - \frac{1}{2}z\]Remember that when setting these kinds of limits up we go from back to front and so the paraboloid will be the lower limit since it is the surface that is in the “back” of the solid while \(x = 1\) is the “front” of the solid and so is the upper limit.
With these limits we can also get the triple integral at least partially set up as follows.
\[\iiint\limits_{E}{{15z\,dV}} = \iint\limits_{D}{{\left[ {\int_{{2 - \frac{1}{2}y - \frac{1}{2}z}}^{{5 - y - \frac{1}{2}z}}{{15z\,dx}}} \right]\,dA}}\] Show Step 3Next, we’ll need limits for \(D\) so we can finish setting up the integral. As noted above the region \(D\) is just the bounded region given in the problem statement. For reference purposes here is a copy of the sketch of \(D\) we gave in the Step 1.

As we can see this region could be integrated in either order but regardless of the order one of the limits will be a quadratic term and one will be a square root. Therefore, we might as well take use the limits as they were given in the problem statement.
So, here are the limits for \(D\).
\[\begin{array}{c}0 \le y \le 1\\ 2{y^2} \le z \le \sqrt {4y} \end{array}\]With these limits plugged into the integral we now have,
\[\iiint\limits_{E}{{15z\,dV}} = \int_{0}^{1}{{\int_{{2{y^2}}}^{{\sqrt {4y} }}{{\int_{{2 - \frac{1}{2}y - \frac{1}{2}z}}^{{5 - y - \frac{1}{2}z}}{{15z\,dx}}\,dz}}\,dy}}\] Show Step 4Okay, now all we need to do is evaluate the integral. Here is the \(x\) integration.
\[\begin{align*}\iiint\limits_{E}{{15z\,dV}} & = \int_{0}^{1}{{\int_{{2{y^2}}}^{{\sqrt {4y} }}{{\left. {\left( {15zx} \right)} \right|_{2 - \frac{1}{2}y - \frac{1}{2}z}^{5 - y - \frac{1}{2}z}\,dz}}\,dy}}\\ & = \int_{0}^{1}{{\int_{{2{y^2}}}^{{\sqrt {4y} }}{{15z\left( {3 - \frac{1}{2}y} \right)\,dz}}\,dy}}\end{align*}\] Show Step 5Now let’s do the \(z\) integration.
\[\begin{align*}\iiint\limits_{E}{{15z\,dV}} & = \int_{0}^{1}{{\left. {\frac{{15}}{2}{z^2}\left( {3 - \frac{1}{2}y} \right)} \right|_{2{y^2}}^{\sqrt {4y} }\,dy}}\\ & = \int_{0}^{1}{{15{y^5} - 90{y^4} - 15{y^2} + 90y\,dy}}\end{align*}\] Show Step 6Finally, let’s do the \(y\) integration.
\[\iiint\limits_{E}{{15z\,dV}} = \left. {\left( {\frac{5}{2}{y^6} - 18{y^5} - 5{y^3} + 45{y^2}} \right)} \right|_0^1 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{49}}{2}}}\]So, once we got the limits all set up, the integration for this problem wasn’t too bad. That will often be the case with these problems. Getting the limits for the integrals set up will often, but not always, be the hardest part of the problem. Once the limits do get set up the integration is often pretty simple and there is no doubt that visualizing the region and getting the limits set up for this problem was probably more difficult that with many of the other problems.